2.4. Glossary
2.4.1. English
- Accuracy (error rate)
The rate of correct (incorrect) predictions made by the model over a data set (cf. coverage). Accuracy is usually estimated by using an independent test set that was not used at any time during the learning process. More complex accuracy estimation techniques, such as cross-validation and the bootstrap, are commonly used, especially with data sets containing a small number of instances.
- Association learning
Techniques that find conjunctive implication rules of the form "\(X\) and \(Y\) implies \(A\) and \(B\) " (associations) that satisfy given criteria. The conventional association algorithms are sound and complete methods for finding all associations that satisfy criteria for minimum support (at least a specified fraction of the instances must satisfy both sides of the rule) and minimum confidence (at least a specified fraction of instances satisfying the left hand side, or antecedent, must satisfy the right hand side, or consequent).
- Attribute (field, variable, feature)
A quantity describing an instance. An attribute has a domain defined by the attribute type, which denotes the values that can be taken by an attribute. The following domain types are common:
- Categorical
A finite number of discrete values. The type nominal denotes that there is no ordering between the values, such as last names and colors. The type ordinal denotes that there is an ordering, such as in an attribute taking on the values low, medium, or high.
- Continuous (quantitative)
Commonly, subset of real numbers, where there is a measurable difference between the possible values. Integers are usually treated as continuous in practical problems.
A feature is the specification of an attribute and its value. For example, color is an attribute. "Color is blue" is a feature of an example. Many transformations to the attribute set leave the feature set unchanged (for example, regrouping attribute values or transforming multi-valued attributes to binary attributes). Some authors use feature as a synonym for attribute (e.g., in feature-subset selection).
- Classification
Process related to categorization, the process in which ideas and objects are recognized, differentiated, and understood.
- Classifier
A mapping from unlabeled instances to (discrete) classes. Classifiers have a form (e.g., decision tree) plus an interpretation procedure (including how to handle unknowns, etc.). Some classifiers also provide probability estimates (scores), which can be threshold to yield a discrete class decision thereby taking into account a utility function.
- Cluster
Group of loosely coupled objects that belongs to the same category
- Confusion matrix
A matrix showing the predicted and actual classifications. A confusion matrix is of size \(LxL\) , where L is the number of different label values. The following confusion matrix is for \(L=2\) :
actual / predicted
negative
positive
Negative
a
b
Positive
c
d
The following terms are defined for a two by two confusion matrix:
- Accuracy
\((a+d) / (a+b+c+d)\)
- True positive rate (Recall, Sensitivity)
\(d / (c+d)\)
- True negative rate (Specificity)
\(a / (a+b)\)
- Precision
\(d / (b+d)\)
- False positive rate
\(b / (a+b)\)
- False negative rate
\(c / (c+d)\)
- Coverage
The proportion of a data set for which a classifier makes a prediction. If a classifier does not classify all the instances, it may be important to know its performance on the set of cases for which it is "confident" enough to make a prediction.
- Cost (utility/loss/payoff)
A measurement of the cost to the performance task (and/or benefit) of making a prediction Y' when the actual label is y. The use of accuracy to evaluate a model assumes uniform costs of errors and uniform benefits of correct classifications.
- Cross-validation
A method for estimating the accuracy (or error) of an inducer by dividing the data into k mutually exclusive subsets (the "folds") of approximately equal size. The inducer is trained and tested \(k\) times. Each time it is trained on the data set minus a fold and tested on that fold. The accuracy estimate is the average accuracy for the k folds.
- Data cleaning/cleansing
The process of improving the quality of the data by modifying its form or content, for example by removing or correcting data values that are incorrect. This step usually precedes the machine learning step, although the knowledge discovery process may indicate that further cleaning is desired and may suggest ways to improve the quality of the data. For example, learning that the pattern Wife implies Female from the census sample at UCI has a few exceptions may indicate a quality problem.
- Data mining
The term data mining is somewhat overloaded. It sometimes refers to the whole process of knowledge discovery and sometimes to the specific machine learning phase.
- Data set
A schema and a set of instances matching the schema. Generally, no ordering on instances is assumed. Most machine learning work uses a single fixed-format table.
- Decision Boundary
In a statistical-classification problem with two classes, a decision boundary or decision surface is a hyper-surface that partitions the underlying vector space into two sets, one for each class. The classifier will classify all the points on one side of the decision boundary as belonging to one class and all those on the other side as belonging to the other class.
A decision boundary is the region of a problem space in which the output label of a classifier is ambiguous.
- Dimension
An attribute or several attributes that together describe a property. For example, a geographical dimension might consist of three attributes: country, state, city. A time dimension might include 5 attributes: year, month, day, hour, minute.
- Discriminative model
Class of models used in machine learning for modeling the dependence of unobserved (target) variables \(y\) on observed variables \(x\). Within a probabilistic framework, this is done by modeling the conditional probability distribution \(P(y|x)\), which can be used for predicting \(y\) from \(x\).
Discriminative models, as opposed to generative models, do not allow one to generate samples from the joint distribution of observed and target variables. However, for tasks such as classification and regression that do not require the joint distribution, discriminative models can yield superior performance (in part because they have fewer variables to compute). On the other hand, generative models are typically more flexible than discriminative models in expressing dependencies in complex learning tasks. In addition, most discriminative models are inherently supervised and cannot easily support unsupervised learning. Application-specific details ultimately dictate the suitability of selecting a discriminative versus generative model.
- Error rate
See Accuracy.
- Example
See Instance.
- Feature
See Attribute.
- Feature vector (record, tuple)
A list of features describing an instance.
- Field
See Attribute.
- Generative Model
In statistical classification, including machine learning, two main approaches are called the generative approach and the discriminative approach. These compute classifiers by different approaches, differing in the degree of statistical modelling. Terminology is inconsistent,[a] but three major types can be distinguished, following (Jebara 2004):
Given an observable variable \(X\) and a target variable \(Y\), a generative model is a statistical model of the joint probability distribution on \(X × Y\), \(P(X,Y)\),
A discriminative model is a model of the conditional probability of the target \(Y\), given an observation \(x\), symbolically, \(P(Y|X=x)\),
Classifiers computed without using a probability model are also referred to loosely as "discriminative".
- i.i.d. sample
A set of independent and identically distributed instances.
- Inducer / induction algorithm
An algorithm that takes as input specific instances and produces a model that generalizes beyond these instances.
- Instance (example, case, record)
A single object of the world from which a model will be learned, or on which a model will be used (e.g., for prediction). In most machine learning work, instances are described by feature vectors; some work uses more complex representations (e.g., containing relations between instances or between parts of instances).
- Knowledge discovery
The non-trivial process of identifying valid, novel, potentially useful, and ultimately understandable patterns in data. This is the definition used in "Advances in Knowledge Discovery and Data Mining", 1996, by Fayyad, Piatetsky-Shapiro, and Smyth.
- Learning Algorithm
Procedure that creates classifiers. Finds patterns in training data.
- Loss
See Cost.
- Machine learning
In Knowledge Discovery, machine learning is most commonly used to mean the application of induction algorithms, which is one step in the knowledge discovery process. This is similar to the definition of empirical learning or inductive learning in Readings in Machine Learning by Shavlik and Dietterich. Note that in their definition, training examples are "externally supplied", whereas here they are assumed to be supplied by a previous stage of the knowledge discovery process. Machine Learning is the field of scientific study that concentrates on induction algorithms and on other algorithms that can be said to "learn".
- Missing value
The value for an attribute is not known or does not exist. There are several possible reasons for a value to be missing, such as: it was not measured; there was an instrument malfunction; the attribute does not apply, or the attribute's value cannot be known. Some algorithms have problems dealing with missing values.
- Model
- Estimator
A structure and corresponding interpretation that summarizes or partially summarizes a set of data, for description or prediction. Most inductive algorithms generate models that can then be used as classifiers, as regressors, as patterns for human consumption, and/or as input to subsequent stages of the KDD process.
- Model deployment
The use of a learned model. Model deployment usually denotes applying the model to real data.
- Observation
One row in features and labels table. For example Iris dataset has 150 observations.
- Out-of-sample data
Data that is not in Observation. In most cases that would be the data to predict.
- OLAP (MOLAP, ROLAP)
On-Line Analytical Processing. Usually synonymous with MOLAP (multi-dimensional OLAP). OLAP engines facilitate the exploration of data along several (predetermined) dimensions. OLAP commonly uses intermediate data structures to store pre-calculated results on multidimensional data, allowing fast computations. ROLAP (relational OLAP) refers to performing OLAP using relational databases.
- Overfitting
Models that overfit learns to recognize noise from the signal, than the data.
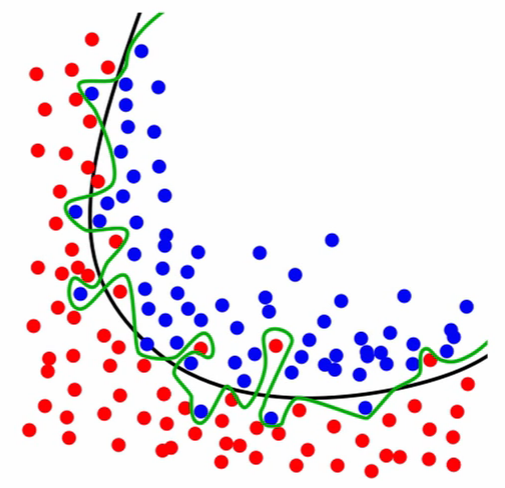
Figure 2.25. Black line represents the decision boundary and represents the signal. Green line represents overfitted model which learned the noise.
- Preprocessing
Is the module used to do some cleaning/scaling of data prior to machine learning.
- Record
See Feature vector.
- Regression
Is a form of supervised machine learning, which is where the scientist teaches the machine by showing it features and then showing it was the correct answer is, over and over, to teach the machine. Once the machine is taught, the scientist will usually "test" the machine on some unseen data, where the scientist still knows what the correct answer is, but the machine doesn't. The machine's answers are compared to the known answers, and the machine's accuracy can be measured. If the accuracy is high enough, the scientist may consider actually employing the algorithm in the real world.
- Regressor
A mapping from unlabeled instances to a value within a predefined metric space (e.g., a continuous range).
- Resubstitution accuracy (error/loss)
The accuracy (error/loss) made by the model on the training data.
- Schema
A description of a data set's attributes and their properties.
- Sensitivity
True positive rate (see Confusion matrix).
- Specificity
True negative rate (see Confusion matrix).
- Supervised learning
Techniques used to learn the relationship between independent attributes and a designated dependent attribute (the label). Most induction algorithms fall into the supervised learning category.
- Tuple
See Feature vector.
- Unsupervised learning
Learning techniques that group instances without a pre-specified dependent attribute. Clustering algorithms are usually unsupervised.
- Utility
See Cost.
2.4.2. Polish
- Błąd I rodzaju (prawdopodobieństwo błędu)
Popełniany, gdy odrzucamy hipotezę zerową. Jest to ryzyko odrzucenia prawdziwej hipotezy zerowej. Np. p=0,05 oznacza, że gdybyśmy nieskończenie wiele razy pobierali próby tej samej wielkości z populacji generalnej o tej samej średniej, to średnio 5 razy na 100 przeprowadzonych testów odrzucilibyśmy hipotezę zerową. Obserwowane różnice między próbami mogą być dziełem przypadku.
- Błąd II rodzaju
Popełniamy, gdy przyjmujemy hipotezę zerową. Jest to ryzyko przyjęcia fałszywej hipotezy zerowej.
- Błąd standardowy
Odchylenie standardowe średnich z prób (gdybyśmy wiele razy pobierali próby tej samej wielkości z tej samej populacji generalnej, liczyli z nich średnie, a potem odchylenie standardowe tych średnich). Błąd standardowy zwykle nie da się wyliczyć bezpośrednio – szacuje się go na podstawie odchylenia standardowego obliczonego z pojedynczej próby, dzieląc to odchylenie przez pierwiastek z wielkości tej próby (odchylenie standardowe średnich jest o pierwiastek z N mniejsze niż odchylenie standardowe pomiarów)
- Hipoteza alternatywna
hipoteza przeciwna do hipotezy zerowej, którą przyjmujemy odrzucając hipotezę zerową.
- Hipoteza zerowa
hipoteza statystyczna, skonstruowana tak by dało się ją obalić. Zwykle stwierdzenie przeciwne do tego co chcemy udowodnić w wyniku testowania hipotez (o braku różnic/zależności). Np. jeżeli chcemy zbadać różnice w masie ciała między płciami, H0 zakłada brak różnic. Jeżeli w toku analiz H0 zostanie odrzucona, będziemy mogli przyjąć iż płcie różnią się masą.
- Istotność statystyczna
różnice/zależności, które w wyniku testowania hipotez uważamy, że są cechą populacji generalnej (p równe lub mniejsze niż założony poziom istotności).
- Kodowanie
zmiana położenia średniej, poprzez operacje typu dodawanie, odejmowanie, dzielenie i mnożenie. Kodowanie nie zmienia kształtu rozkładu
- Korelacja
metoda służąca do badania siły zależności między dwiema zmiennymi wyrażonymi w skali interwałowej (ciągłymi). Przyjmuje wartości między -1 a 1, przy czym r=0 to brak związku, a wartości 1 i -1 oznaczają, że jedna zmienna wyjaśnia całkowicie zmienność obserwowaną w drugiej zmiennej.
- Liczba stopni swobody
Jak dużo niezależnych obserwacji składających się na próbę możemy użyć do oszacowania danego parametru statystycznego. Ile pomiarów w próbie może przyjmować dowolne wartości (nie są zdeterminowane przez oszacowane parametry).
- Odchylenie standardowe
Miara rozproszenia pomiarów wokół średniej. Determinuje kształt rozkładu normalnego (jest parametrem tego rozkładu). Zwykle nie jest znane dla populacji generalnej, obliczane na podstawie próby staje się oszacowaniem dla populacji.
- Parametr
np. średnia czy odchylenie standardowe w populacji generalnej. Zwykle nieznane dla populacji i szacowane (estymowane) na podstawie próby. Decyduje o wyglądzie rozkładu statystycznego.
- Poziom istotności
Maksymalna dopuszczalna wartość prawdopodobieństwa, że w procedurze testowania hipotez odrzucimy prawdziwą H0 (maksymalna wartość błędu pierwszego rodzaju jaki dopuszczamy). Nie odrzucimy H0 jeśli wartość błędu I rodzaju miałaby być większa.
- Próba
Losowo wybrane elementy populacji generalnej.
- Próba reprezentatywna
to taka w której każdy element populacji ma taką samą szansę pojawienia się w próbie (że każda wartość ma szansę pojawienia się w próbie z prawdopodobieństwem odpowiadającym częstości występowania w populacji takiej wartości). Próbę pobieramy po to wnioskować o całej populacji, gdy cechy tej populacji nie są możliwe do bezpośredniego oszacowania.
- Przedział ufności
przedział wartości, w którym z określonym prawdopodobieństwem oczekujemy średnia z populacji generalnej. Wyznaczany na podstawie średniej i odchylenia standardowego w próbie pozwala wnioskować o populacji generalnej (o średniej z tej populacji). Np. stwierdzenie iż 95% przedział ufności dla średniej masy ciała nornic to 25- 35g, oznacza że z 95% ufnością oczekujemy, że średnia masa ciała nornic mieści się w granicach 25g do 35g. Przedział jest tym węższy (z większą dokładnością szacuje położenie średniej z populacji) im próba jest większa i im mniejszą ufność przykładamy do oszacowania tego przedziału.
- Regresja
metoda statystyczna służąca do opisania charakteru zależności między dwiema zmiennymi wyrażonymi w skali interwałowej. Zwykle polega na opisaniu związku między zmiennymi w postaci równania liniowego Y=aX+b, które wyznacza się metodą najmniejszych kwadratów. W przypadku związków przyczynowo-skutkowych regresja pozwala przewidywać wartości zmiennej zależnej na podstawie wartości zmiennej niezależnej.
- Rozkład
Częstość występowania poszczególnych wartości w populacji.
- Rozkład normalny
Rozkład pomiarów wokół średniej w populacji (średnie i odchylenie standardowe są parametrami tego rozkładu).
- Rozkład t-Studenta
Rozkład średnich z prób N-elementowych od średniej ze średnich z prób (średniej z populacji generalnej; parametrem jest liczna stopni swobody).
- Rozkład dwumianowy
Rozkład częstości sukcesów w próbie N-elementowej (operuje na skali nominalnej dychotomicznej, parametry: wielkość próby, liczba sukcesów, częstość danej kategorii w populacji generalnej).
- Standaryzacja danych
operacja mająca na celu taką obróbkę danych, żeby dane pochodzące z różnych prób/populacji były ze sobą porównywalnej. Zwykle polega na obliczeniu różnicy między wartością pomiaru a średnią z próby i podzielenie jej przez odchylenie standardowe z tej próby. Dla danych standaryzowanych średnia wynosi zero natomiast odchylenie standardowe równa się jeden.
- Statystyka
wartość obliczona na podstawie próby, np. średnia, odchylenie standardowe, obliczona w procesie testowania hipotez wartość t, r itp. Statystykę można traktować pod pewnymi warunkami jako oszacowanie parametru (estymator).
- Skala pomiarowa
Skala interwałowa: pomiary wynikające z mierzenia, ważenia, zwykle wyrażone w liczbach rzeczywistych. Skala porządkowa: kolejność, rangi, zwykle wyrażone w liczbach całkowitych. Skala nominalna: dane w postaci liczebności w jasno zdefiniowanych kategoriach (np. płeć).
- Test dwustronny
nie można z góry przewidzieć kierunku testowanych różnic/zależności. Korzysta z dwóch stron rozkładu (wartości krytyczne znajdują się po obu stronach rozkładu). Taki test jest testem słabszym niż test jednostronny.
- Test jednostronny
z góry można przewidzieć kierunek różnic/zależności (o ile w ogóle istnieją). Stosowany zwykle w badaniach jakości – czy spełnione są standardy/normy (np. jakość żywności, wody, produktów). Korzysta z jednej określonej strony rozkładu (wartości krytyczne znajdują się tylko po jednej stronie rozkładu). Test mocniejszy.
- Test statystyczny
metoda służąca określeniu, czy założona hipoteza zerowa jest prawdziwa czy fałszywa. W wyniku testowania hipotezy staramy się ją odrzucić na podstawie porównania statystyki testu (wynikającej z obliczeń) z wartością krytyczną.
- Test parametryczny
oparty na parametrach rozkładu normalnego (liczymy w nim średnią i odchylenie standardowe) w odróżnieniu od testu nieparametrycznego, który nie musi spełniać założenia normalności rozkładu w populacji generalnej.
- Transformacja
Zmiana wartości zmiennej poprzez zastosowanie operacji matematycznej w postaci funkcji matematycznych. Np. potęgowanie, pierwiastkowanie, logarytmowanie itp. Transformacja zmienia kształt rozkładu (wartość zmienia się nieproporcjonalnie).
- Wariancja
miara rozproszenia danych wokół średniej. Inaczej średnie odchylenie kwadratów od średniej (suma podniesionych do kwadratu różnic między wartością każdego pomiaru w próbie a średnią, podzielona przez wielkość próby - 1)
- Wartość krytyczna
Wartość z rozkładu teoretycznego, która dla założonego poziomu istotności stanowi wartość graniczną, przy której będziemy odrzucać hipotezę zerową.
- Zmienna niezależna
Zmienna która wpływa na inną zmienna (kształtuje zmienność zmiennej zależnej). Np. w równaniu Y=aX+b, X jest zmienną niezależną.
- Zmienna zależna
Jej zmienność chcemy wyjaśnić wpływem innej zmiennej (zmiennej niezależnej). Np. w równaniu Y=aX+b, Y jest zmienną zależną.