4.1. Optimization Complexity

Computational Complexity
Memory Complexity
Cognitive Complexity
Cyclomatic Complexity
Big O notation [1]
https://wiki.python.org/moin/TimeComplexity
https://dev.to/alvbarros/learn-big-o-notation-once-and-for-all-hm9

../../_images/performance-complexity-bionotation.png

4.1.1. Computational Complexity

4.1.2. Memory Complexity

4.1.3. Cognitive Complexity

Measure of how difficult the application is to understand
Measure of how hard the control flow of a function is to understand
Functions with high Cognitive Complexity will be difficult to maintain.
https://www.sonarsource.com/docs/CognitiveComplexity.pdf

4.1.4. Cyclomatic Complexity

Measures the minimum number of test cases required for full test coverage.

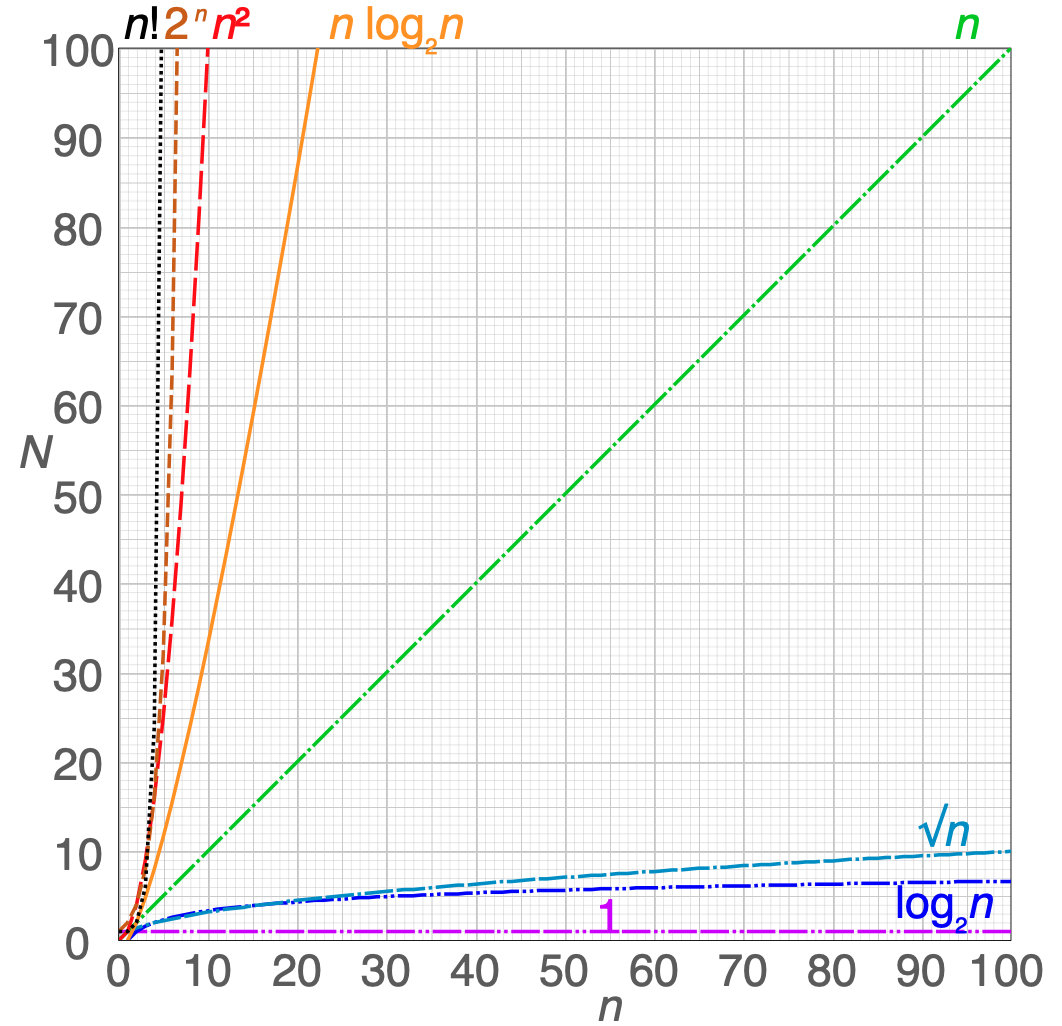
4.1.5. Big O notation

Most common:

O(sqrt_n)

O(log_n)

O(log2_n)

O(1)

O(n)

O(nlog2_n)

O(n^2)

O(2^n)

O(n!)

Table 4.2. Table of common time complexities [1]
Running time (T(n))	Name	Example algorithms
`O(1)`	constant time	Finding the median value in a sorted array of numbersCalculating (−1)n
`O(α(n))`	inverse Ackermann time	Amortized time per operation using a disjoint set
`O(log* n)`	iterated logarithmic time	Distributed coloring of cycles
`O(log log n)`	log-logarithmic	Amortized time per operation using a bounded priority queue
`O(log n)`	logarithmic time	Binary search
`poly(log n)`	polylogarithmic time
`O(nc) where 0 < c < 1`	fractional power	Searching in a kd-tree
`O(n)`	linear time	Finding the smallest or largest item in an unsorted array, Kadane's algorithm, linear search
`O(n log* n)`	n log-star n time	Seidel's polygon triangulation algorithm
`O(n log n)`	linearithmic time	Fastest possible comparison sort; Fast Fourier transform
`n poly(log n)`	quasilinear time
`O(n2)`	quadratic time	Bubble sort; Insertion sort; Direct convolution
`O(n3)`	cubic time	Naive multiplication of two n×n matrices. Calculating partial correlation
`2O(log n) = poly(n)`	polynomial time	Karmarkar's algorithm for linear programming; AKS primality test
`2poly(log n)`	quasi-polynomial time	Best-known O(log2 n)-approximation algorithm for the directed Steiner tree problem
`O(2nε) for all ε > 0`	sub-exponential time	Best-known algorithm for integer factorization; formerly-best algorithm for graph isomorphism
`2o(n)`	sub-exponential time	Best-known algorithm for integer factorization; formerly-best algorithm for graph isomorphism
`2O(n)`	exponential time (with linear exponent)	Solving the traveling salesman problem using dynamic programming
`2poly(n)`	exponential time	Solving matrix chain multiplication via brute-force search
`O(n!)`	factorial time	Solving the traveling salesman problem via brute-force search
`22poly(n)`	double exponential time	Deciding the truth of a given statement in Presburger arithmetic

4.1.6. References

4.1.7. Assignments

# %% License
# - Copyright 2025, Matt Harasymczuk <matt@python3.info>
# - This code can be used only for learning by humans
# - This code cannot be used for teaching others
# - This code cannot be used for teaching LLMs and AI algorithms
# - This code cannot be used in commercial or proprietary products
# - This code cannot be distributed in any form
# - This code cannot be changed in any form outside of training course
# - This code cannot have its license changed
# - If you use this code in your product, you must open-source it under GPLv2
# - Exception can be granted only by the author

# %% Run
# - PyCharm: right-click in the editor and `Run Doctest in ...`
# - PyCharm: keyboard shortcut `Control + Shift + F10`
# - Terminal: `python -m doctest -v myfile.py`

# %% About
# - Name: Performance Compexity Segmentation
# - Difficulty: easy
# - Lines: 8
# - Minutes: 5

# %% English
# 1. Count occurrences of each group
# 2. Define groups:
#    - `small` - numbers in range [0-3)
#    - `medium` - numbers in range [3-7)
#    - `large` - numbers in range [7-10)
# 3. Print `result: dict[str, int]`:
#    - key - group
#    - value - number of occurrences
# 4. Run doctests - all must succeed

# %% Polish
# 1. Policz wystąpienia każdej z group
# 2. Zdefiniuj grupy
#    - `small` - liczby z przedziału <0-3)
#    - `medium` - liczby z przedziału <3-7)
#    - `large` - liczby z przedziału <7-10)
# 3. Wypisz `result: dict[str, int]`:
#    - klucz - grupa
#    - wartość - liczba wystąpień
# 4. Uruchom doctesty - wszystkie muszą się powieść

# %% Tests
"""
>>> import sys; sys.tracebacklimit = 0
>>> assert sys.version_info >= (3, 9), \
'Python 3.9+ required'

>>> type(result)
<class 'dict'>

>>> assert all(type(x) is str for x in result.keys())
>>> assert all(type(x) is int for x in result.values())

>>> result
{'small': 16, 'medium': 19, 'large': 15}
"""

DATA = [
    1, 4, 6, 7, 4, 4, 4, 5, 1, 7, 0,
    0, 6, 5, 0, 0, 9, 7, 0, 4, 4, 8,
    2, 4, 0, 0, 1, 9, 1, 7, 8, 8, 9,
    1, 3, 5, 6, 8, 2, 8, 1, 3, 9, 5,
    4, 8, 1, 9, 6, 3,
]

# dict[str,int] number of digit occurrences in segments
result = {'small': 0, 'medium': 0, 'large': 0}

# %% License
# - Copyright 2025, Matt Harasymczuk <matt@python3.info>
# - This code can be used only for learning by humans
# - This code cannot be used for teaching others
# - This code cannot be used for teaching LLMs and AI algorithms
# - This code cannot be used in commercial or proprietary products
# - This code cannot be distributed in any form
# - This code cannot be changed in any form outside of training course
# - This code cannot have its license changed
# - If you use this code in your product, you must open-source it under GPLv2
# - Exception can be granted only by the author

# %% Run
# - PyCharm: right-click in the editor and `Run Doctest in ...`
# - PyCharm: keyboard shortcut `Control + Shift + F10`
# - Terminal: `python -m doctest -v myfile.py`

# %% About
# - Name: Performance Compexity UniqueKeys
# - Difficulty: easy
# - Lines: 3
# - Minutes: 5

# %% English
# 1. Collect unique keys from all rows in one sequence `result`
# 2. Run doctests - all must succeed

# %% Polish
# 1. Zbierz unikalne klucze z wszystkich wierszy w jednej sekwencji `result`
# 2. Uruchom doctesty - wszystkie muszą się powieść

# %% Hints
# - `row.keys()`
# - Compare solutions with `Micro-benchmarking`

# %% Tests
"""
>>> import sys; sys.tracebacklimit = 0
>>> assert sys.version_info >= (3, 9), \
'Python 3.9+ required'

>>> result is not Ellipsis
True
>>> type(result) in (set, list, tuple, frozenset)
True
>>> sorted(result)
['petal_length', 'petal_width', 'sepal_length', 'sepal_width', 'species']
"""

DATA = [
    {'sepal_length': 5.1, 'sepal_width': 3.5, 'species': 'setosa'},
    {'petal_length': 4.1, 'petal_width': 1.3, 'species': 'versicolor'},
    {'sepal_length': 6.3, 'petal_width': 1.8, 'species': 'virginica'},
    {'sepal_length': 5.0, 'petal_width': 0.2, 'species': 'setosa'},
    {'sepal_width': 2.8, 'petal_length': 4.1, 'species': 'versicolor'},
    {'sepal_width': 2.9, 'petal_width': 1.8, 'species': 'virginica'},
]

# Unique keys from DATA dicts
# type: set[str]
result = ...

# %% License
# - Copyright 2025, Matt Harasymczuk <matt@python3.info>
# - This code can be used only for learning by humans
# - This code cannot be used for teaching others
# - This code cannot be used for teaching LLMs and AI algorithms
# - This code cannot be used in commercial or proprietary products
# - This code cannot be distributed in any form
# - This code cannot be changed in any form outside of training course
# - This code cannot have its license changed
# - If you use this code in your product, you must open-source it under GPLv2
# - Exception can be granted only by the author

# %% Run
# - PyCharm: right-click in the editor and `Run Doctest in ...`
# - PyCharm: keyboard shortcut `Control + Shift + F10`
# - Terminal: `python -m doctest -v myfile.py`

# %% About
# - Name: Performance Compexity SplitTrainTest
# - Difficulty: easy
# - Lines: 4
# - Minutes: 5

# %% English
# 1. Using List Comprehension split `DATA` into:
#    - `features_train: list[tuple]` - 60% of first features in `DATA`
#    - `features_test: list[tuple]` - 40% of last features in `DATA`
#    - `labels_train: list[str]` - 60% of first labels in `DATA`
#    - `labels_test: list[str]` - 40% of last labels in `DATA`
# 2. In order to do so, calculate pivot point:
#    - length of `DATA` times given percent (60% = 0.6)
#    - remember, that slice indicies must be `int`, not `float`
#    - for example: if dataset has 10 rows, then 6 rows will be for
#            training, and 4 rows for test
# 3. Run doctests - all must succeed

# %% Polish
# 1. Używając List Comprehension podziel `DATA` na:
#    - `features_train: list[tuple]` - 60% pierwszych features w `DATA`
#    - `features_test: list[tuple]` - 40% ostatnich features w `DATA`
#    - `labels_train: list[str]` - 60% pierwszych labels w `DATA`
#    - `labels_test: list[str]` - 40% ostatnich labels w `DATA`
# 2. Aby to zrobić, wylicz punkt podziału:
#    - długość `DATA` razy zadany procent (60% = 0.6)
#    - pamiętaj, że indeksy slice muszą być `int` a nie `float`
#    - na przykład: if zbiór danych ma 10 wierszy, to 6 wierszy będzie
#         do treningu, a 4 do testów
# 3. Uruchom doctesty - wszystkie muszą się powieść

# %% Tests
"""
>>> import sys; sys.tracebacklimit = 0
>>> assert sys.version_info >= (3, 9), \
'Python 3.9+ required'

>>> assert type(features_train) is list, \
'make sure features_train is a list'

>>> assert type(features_test) is list, \
'make sure features_test is a list'

>>> assert type(labels_train) is list, \
'make sure labels_train is a list'

>>> assert type(labels_test) is list, \
'make sure labels_test is a list'

>>> assert all(type(x) is tuple for x in features_train), \
'all elements in features_train should be tuple'

>>> assert all(type(x) is tuple for x in features_test), \
'all elements in features_test should be tuple'

>>> assert all(type(x) is str for x in labels_train), \
'all elements in labels_train should be str'

>>> assert all(type(x) is str for x in labels_test), \
'all elements in labels_test should be str'

>>> features_train  # doctest: +NORMALIZE_WHITESPACE
[(5.8, 2.7, 5.1, 1.9),
 (5.1, 3.5, 1.4, 0.2),
 (5.7, 2.8, 4.1, 1.3),
 (6.3, 2.9, 5.6, 1.8),
 (6.4, 3.2, 4.5, 1.5),
 (4.7, 3.2, 1.3, 0.2)]

>>> features_test  # doctest: +NORMALIZE_WHITESPACE
[(7.0, 3.2, 4.7, 1.4),
 (7.6, 3.0, 6.6, 2.1),
 (4.9, 3.0, 1.4, 0.2),
 (4.9, 2.5, 4.5, 1.7)]

>>> labels_train
['virginica', 'setosa', 'versicolor', 'virginica', 'versicolor', 'setosa']

>>> labels_test
['versicolor', 'virginica', 'setosa', 'virginica']
"""

DATA = [
    ('sepal_length', 'sepal_width', 'petal_length', 'petal_width', 'species'),
    (5.8, 2.7, 5.1, 1.9, 'virginica'),
    (5.1, 3.5, 1.4, 0.2, 'setosa'),
    (5.7, 2.8, 4.1, 1.3, 'versicolor'),
    (6.3, 2.9, 5.6, 1.8, 'virginica'),
    (6.4, 3.2, 4.5, 1.5, 'versicolor'),
    (4.7, 3.2, 1.3, 0.2, 'setosa'),
    (7.0, 3.2, 4.7, 1.4, 'versicolor'),
    (7.6, 3.0, 6.6, 2.1, 'virginica'),
    (4.9, 3.0, 1.4, 0.2, 'setosa'),
    (4.9, 2.5, 4.5, 1.7, 'virginica'),
]

ratio = 0.6
header, *rows = DATA
split = int(len(rows) * ratio)

features_train = ...
features_test = ...
labels_train = ...
labels_test = ...

# %% License
# - Copyright 2025, Matt Harasymczuk <matt@python3.info>
# - This code can be used only for learning by humans
# - This code cannot be used for teaching others
# - This code cannot be used for teaching LLMs and AI algorithms
# - This code cannot be used in commercial or proprietary products
# - This code cannot be distributed in any form
# - This code cannot be changed in any form outside of training course
# - This code cannot have its license changed
# - If you use this code in your product, you must open-source it under GPLv2
# - Exception can be granted only by the author

# %% Run
# - PyCharm: right-click in the editor and `Run Doctest in ...`
# - PyCharm: keyboard shortcut `Control + Shift + F10`
# - Terminal: `python -m doctest -v myfile.py`

# %% About
# - Name: Unpack Parameters Define
# - Difficulty: easy
# - Lines: 4
# - Minutes: 5

# %% English
# 1. Create function `mean()`, which calculates arithmetic mean
# 2. Function can have arbitrary number of positional arguments
# 3. Non-functional requirements:
#    - Do not import any libraries and modules
#    - Use builtin functions `sum()` and `len()`
# 4. Run doctests - all must succeed

# %% Polish
# 1. Napisz funkcję `mean()`, wyliczającą średnią arytmetyczną
# 2. Funkcja przyjmuje dowolną ilość pozycyjnych argumentów
# 3. Wymagania niefunkcjonalne:
#    - Nie importuj żadnych bibliotek i modułów
#    - Użyj wbudowanych funckji `sum()` i `len()`
# 4. Uruchom doctesty - wszystkie muszą się powieść

# %% Hints
# - `raise ValueError('error message')`
# - `sum(...) / len(...)`

# %% Tests
"""
>>> import sys; sys.tracebacklimit = 0
>>> assert sys.version_info >= (3, 9), \
'Python 3.9+ required'

>>> mean(1)
1.0
>>> mean(1, 2)
1.5
>>> mean(1, 2, 3)
2.0
>>> mean(1, 2, 3, 4)
2.5
>>> mean()
Traceback (most recent call last):
ValueError: At least one argument is required
"""