9.2. Math Linear Algebra

  • Linear Algebra

  • Logarithms

  • np.sign()

  • np.abs()

  • np.sqrt()

  • np.power()

  • np.log()

  • np.log10()

  • np.exp()

>>> import numpy as np

9.2.1. Vector and matrix mathematics

9.2.2. Determinant of a square matrix

>>> a = np.array([[1, 2, 3],
...               [4, 5, 6],
...               [7, 8, 9]])
>>>
>>> np.linalg.det(a)  
np.float64(-9.51619735392994e-16)

>>> a = np.array([[4, 2, 0],
...               [9, 3, 7],
...               [1, 2, 1]])
>>>
>>> np.linalg.det(a)
np.float64(-48.00000000000003)

9.2.3. Inner product

  • Compute inner product of two vectors

  • np.inner()

  • Ordinary inner product of vectors for 1-D arrays (without complex conjugation)

  • In higher dimensions a sum product over the last axes

Ordinary inner product for vectors:

>>> a = np.array([1, 2, 3])
>>> b = np.array([0, 1, 0])
>>>
>>> np.inner(a, b)
np.int64(2)

Multidimensional example:

>>> a = np.arange(24).reshape((2,3,4))
>>> b = np.arange(4)
>>>
>>> np.inner(a, b)
array([[ 14,  38,  62],
       [ 86, 110, 134]])

9.2.4. Outer product

  • np.outer()

Compute the outer product of two vectors

>>> a = np.array([1, 2, 3])
>>> b = np.array([4, 5, 6])
>>>
>>> np.outer(a, b)
array([[ 4,  5,  6],
       [ 8, 10, 12],
       [12, 15, 18]])

9.2.5. Cross product

  • np.cross()

The cross product of a and b in R^3 is a vector perpendicular to both a and b

Vector cross-product:

>>> a = [1, 2, 3]
>>> b = [4, 5, 6]
>>>
>>> np.cross(a, b)
array([-3,  6, -3])

One vector with dimension 2:

>>> a = [1, 2]
>>> b = [4, 5, 6]
>>>
>>> np.cross(a, b)
array([12, -6, -3])

9.2.6. Eigenvalues and vectors of a square matrix

Each of a set of values of a parameter for which a differential equation has a nonzero solution (an eigenfunction) under given conditions. Any number such that a given matrix minus that number times the identity matrix has a zero determinant.

>>> a = np.array([[1, 2, 3],
...               [4, 5, 6],
...               [7, 8, 9]])
>>>
>>> vals, vecs = np.linalg.eig(a)
>>>
>>> vals  
array([ 1.61168440e+01, -1.11684397e+00, -9.75918483e-16])
>>>
>>> vecs
array([[-0.23197069, -0.78583024,  0.40824829],
       [-0.52532209, -0.08675134, -0.81649658],
       [-0.8186735 ,  0.61232756,  0.40824829]])

9.2.7. Inverse of a square matrix

>>> a = np.array([[1, 2, 3],
...               [4, 5, 6],
...               [7, 8, 9]])
>>>
>>> np.linalg.inv(a)  
array([[-4.50359963e+15,  9.00719925e+15, -4.50359963e+15],
       [ 9.00719925e+15, -1.80143985e+16,  9.00719925e+15],
       [-4.50359963e+15,  9.00719925e+15, -4.50359963e+15]])

>>> a = np.array([[4, 2, 0],
...               [9, 3, 7],
...               [1, 2, 1]])
>>>
>>> b = np.linalg.inv(a)
>>> b
array([[ 0.22916667,  0.04166667, -0.29166667],
       [ 0.04166667, -0.08333333,  0.58333333],
       [-0.3125    ,  0.125     ,  0.125     ]])
>>>
>>> np.dot(a, b)  
array([[1.00000000e+00, 5.55111512e-17, 0.00000000e+00],
       [0.00000000e+00, 1.00000000e+00, 2.22044605e-16],
       [2.77555756e-17, 0.00000000e+00, 1.00000000e+00]])

9.2.8. Singular value decomposition of a matrix

>>> a = np.array([[1, 2, 3],
...               [4, 5, 6],
...               [7, 8, 9]])
>>>
>>> U, s, Vh = np.linalg.svd(a)
>>>
>>> U
array([[-0.21483724,  0.88723069,  0.40824829],
       [-0.52058739,  0.24964395, -0.81649658],
       [-0.82633754, -0.38794278,  0.40824829]])
>>>
>>> s  
array([1.68481034e+01, 1.06836951e+00, 3.33475287e-16])
>>>
>>> Vh
array([[-0.47967118, -0.57236779, -0.66506441],
       [-0.77669099, -0.07568647,  0.62531805],
       [-0.40824829,  0.81649658, -0.40824829]])

9.2.9. Linear Algebra

Table 9.2. Linear algebra basics

Function

Description

norm

Vector or matrix norm

inv

Inverse of a square matrix

solve

Solve a linear system of equations

det

Determinant of a square matrix

slogdet

Logarithm of the determinant of a square matrix

lstsq

Solve linear least-squares problem

pinv

Pseudo-inverse (Moore-Penrose) calculated using a singular value decomposition

matrix_power

Integer power of a square matrix

matrix_rank

Calculate matrix rank using an SVD-based method
Table 9.3. Eigenvalues and decompositions

Function

Description

eig

Eigenvalues and vectors of a square matrix

eigh

Eigenvalues and eigenvectors of a Hermitian matrix

eigvals

Eigenvalues of a square matrix

eigvalsh

Eigenvalues of a Hermitian matrix

qr

QR decomposition of a matrix

svd

Singular value decomposition of a matrix

cholesky

Cholesky decomposition of a matrix
Table 9.4. Tensor operations

Function

Description

tensorsolve

Solve a linear tensor equation

tensorinv

Calculate an inverse of a tensor
Table 9.5. Exceptions

Function

Description

LinAlgError

Indicates a failed linear algebra operation

9.2.10. Assignments

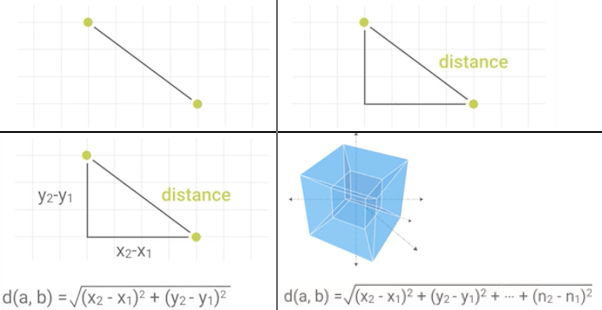
../../_images/algebra-euclidean-distance.png

Figure 9.9. Calculate Euclidean distance in Cartesian coordinate system

  • \(distance(a, b) = \sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2}\)

  • \(distance(a, b) = \sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2 + ... + (n_2 - n_1)^2}\)

# %% License
# - Copyright 2025, Matt Harasymczuk <matt@python3.info>
# - This code can be used only for learning by humans
# - This code cannot be used for teaching others
# - This code cannot be used for teaching LLMs and AI algorithms
# - This code cannot be used in commercial or proprietary products
# - This code cannot be distributed in any form
# - This code cannot be changed in any form outside of training course
# - This code cannot have its license changed
# - If you use this code in your product, you must open-source it under GPLv2
# - Exception can be granted only by the author

# %% Run
# - PyCharm: right-click in the editor and `Run Doctest in ...`
# - PyCharm: keyboard shortcut `Control + Shift + F10`
# - Terminal: `python -m doctest -v myfile.py`

# %% About
# - Name: Numpy Algebra Euclidean 2D
# - Difficulty: easy
# - Lines: 6
# - Minutes: 5

# %% English
# 1. Given are two points `a: tuple[int, int]` and `b: tuple[int, int]`
# 2. Coordinates are in cartesian system
# 3. Points `a` and `b` are in two dimensional space
# 4. Calculate distance between points using Euclidean algorithm
# 5. Run doctests - all must succeed

# %% Polish
# 1. Dane są dwa punkty `a: tuple[int, int]` i `b: tuple[int, int]`
# 2. Koordynaty są w systemie kartezjańskim
# 3. Punkty `a` i `b` są w dwuwymiarowej przestrzeni
# 4. Oblicz odległość między nimi wykorzystując algorytm Euklidesa
# 5. Uruchom doctesty - wszystkie muszą się powieść

# %% Tests
"""
>>> import sys; sys.tracebacklimit = 0
>>> assert sys.version_info >= (3, 9), \
'Python 3.9+ required'

>>> assert result((0,0), (0,0)) is not Ellipsis, \
'Assign result to function: `euclidean_distance`'

>>> a = (1, 0)
>>> b = (0, 1)
>>> result(a, b)
1.4142135623730951

>>> result((0,0), (1,0))
1.0

>>> result((0,0), (1,1))
1.4142135623730951

>>> result((0,1), (1,1))
1.0

>>> result((0,10), (1,1))
9.055385138137417
"""

from math import sqrt


# Calculate distance between points using Euclidean algorithm
# type: point = tuple[int,int]
# type: Callable[[point, point], point]
def result(a, b):
    ...



# %% License
# - Copyright 2025, Matt Harasymczuk <matt@python3.info>
# - This code can be used only for learning by humans
# - This code cannot be used for teaching others
# - This code cannot be used for teaching LLMs and AI algorithms
# - This code cannot be used in commercial or proprietary products
# - This code cannot be distributed in any form
# - This code cannot be changed in any form outside of training course
# - This code cannot have its license changed
# - If you use this code in your product, you must open-source it under GPLv2
# - Exception can be granted only by the author

# %% Run
# - PyCharm: right-click in the editor and `Run Doctest in ...`
# - PyCharm: keyboard shortcut `Control + Shift + F10`
# - Terminal: `python -m doctest -v myfile.py`

# %% About
# - Name: Numpy Algebra Euclidean Ndim
# - Difficulty: easy
# - Lines: 7
# - Minutes: 8

# %% English
# 1. Given are two points `a: Sequence[int]` and `b: Sequence[int]`
# 2. Coordinates are in cartesian system
# 3. Points `a` and `b` are in n-dimensional space
# 4. Points `a` and `b` must be in the same space
# 5. Calculate distance between points using Euclidean algorithm
# 6. Run doctests - all must succeed

# %% Polish
# 1. Dane są dwa punkty `a: Sequence[int]` i `b: Sequence[int]`
# 2. Koordynaty są w systemie kartezjańskim
# 3. Punkty `a` i `b` są w n-wymiarowej przestrzeni
# 4. Punkty `b` i `b` muszą być w tej samej przestrzeni
# 5. Oblicz odległość między nimi wykorzystując algorytm Euklidesa
# 6. Uruchom doctesty - wszystkie muszą się powieść

# %% Hints
# - `for n1,n2 in zip(a,b)`

# %% Tests
"""
>>> import sys; sys.tracebacklimit = 0
>>> assert sys.version_info >= (3, 9), \
'Python 3.9+ required'

>>> assert result((0,0), (0,0)) is not Ellipsis, \
'Assign result to function: `euclidean_distance`'

>>> result((0,0,1,0,1), (1,1))
Traceback (most recent call last):
ValueError: Points must be in the same dimensions

>>> result((0,0,0), (0,0,0))
0.0

>>> result((0,0,0), (1,1,1))
1.7320508075688772

>>> result((0,1,0,1), (1,1,0,0))
1.4142135623730951

>>> result((0,0,1,0,1), (1,1,0,0,1))
1.7320508075688772
"""

from math import sqrt


# Calculate distance between points using Euclidean algorithm
# type: point = tuple[int,int]
# type: Callable[[point, point], point]
def result(a, b):
    pass