10.1. Polynomial About

10.1.1. SetUp

>>> import numpy as np

10.1.2. Defining

Polynomial of degree three:

Ax^3 + Bx^2 + Cx^1 + D = 0
1x^3 + 2x^2 + 3x^1 + 4 = 0

>>> np.poly1d([1, 2, 3, 4])
poly1d([1, 2, 3, 4])

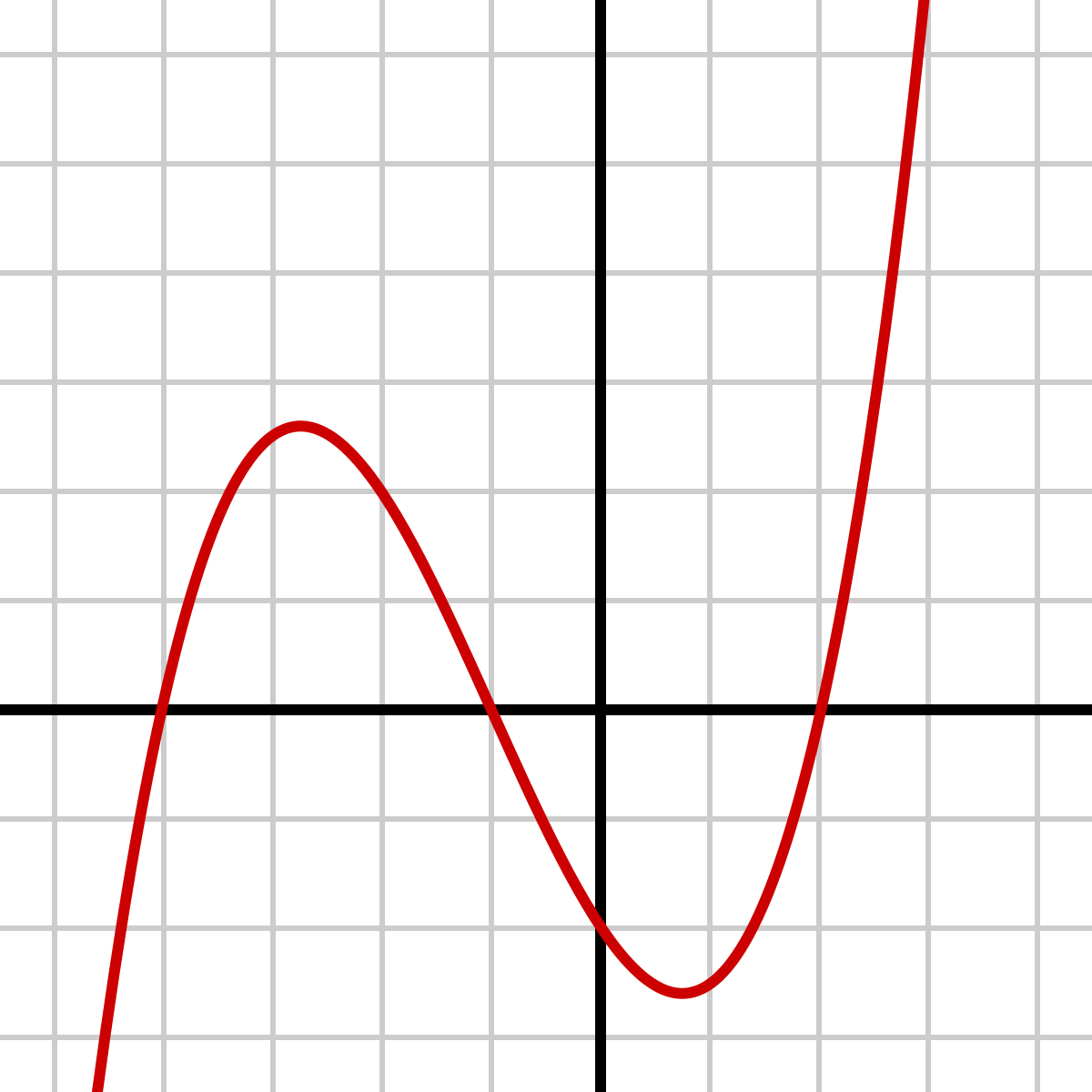
Figure 10.1. Polynomial of degree three Ax^3 + Bx^2 + Cx^1 + D = 0 [1]

Polynomial of degree six:

Ax^6 + Bx^5 + Cx^4 + Dx^3 + Ex^2 + Fx + G = 0
1x^6 + 2x^5 + 3x^4 + 4x^3 + 5x^2 + 6x + 7 = 0

>>> np.poly1d([1, 2, 3, 4, 5, 6, 7])
poly1d([1, 2, 3, 4, 5, 6, 7])

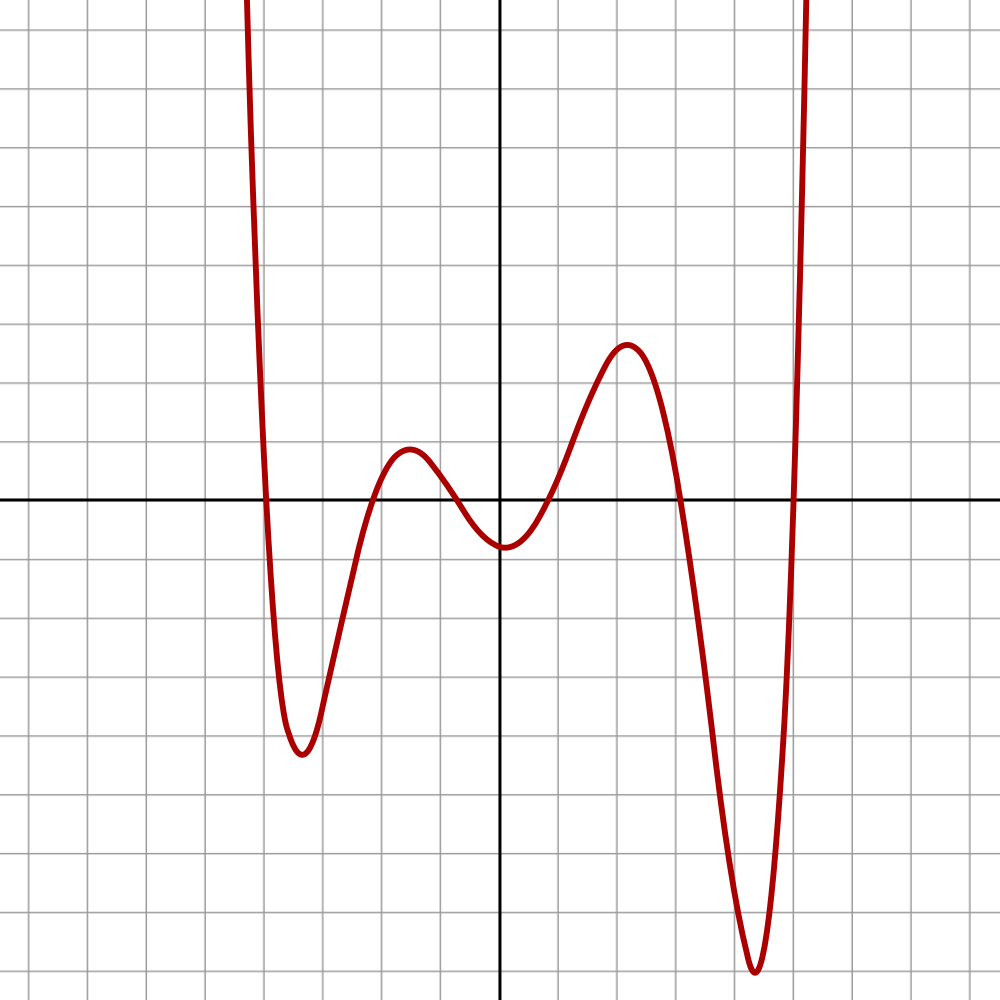
Figure 10.2. Polynomial of degree six Ax^6 + Bx^5 + Cx^4 + Dx^3 + Ex^2 + Fx + G = 0 [1]

10.1.3. Find Coefficients

• Find the coefficients of a polynomial with the given sequence of roots

• Specifying the roots of a polynomial still leaves one degree of freedom, typically represented by an undetermined leading coefficient.

>>> np.poly([0, 0, 0])
array([1., 0., 0., 0.])

>>> np.poly([1, 2])
array([ 1., -3.,  2.])

>>> np.poly([1, 2, 3, 4, 5, 6, 7])
array([ 1.0000e+00, -2.8000e+01,  3.2200e+02, -1.9600e+03,  6.7690e+03,
       -1.3132e+04,  1.3068e+04, -5.0400e+03])

10.1.4. Roots

• Return the roots of a polynomial

>>> np.roots([1, 2])
array([-2.])

>>> np.roots([0, 1, 3])
array([-3.])

>>> np.roots([1, 4, -2, 3]).round(4)
array([-4.5797+0.j    ,  0.2899+0.7557j,  0.2899-0.7557j])

>>> np.roots([ 1, -11, 9, 11, -10]).round(4)  
array([10., -1.,  1.,  1.])

10.1.5. Derivative of a Polynomial

>>> np.polyder([1/4, 1/3, 1/2, 1, 0])
array([1., 1., 1., 1.])

>>> np.polyder([0.25, 0.33333333, 0.5, 1, 0]).round(4)
array([1., 1., 1., 1.])

>>> np.polyder([1, 2, 3, 4])
array([3, 4, 3])

10.1.6. Antiderivative (indefinite integral) of a polynomial

• Return an antiderivative (indefinite integral) of a polynomial

>>> np.polyint([1, 1, 1, 1]).round(4)
array([0.25  , 0.3333, 0.5   , 1.    , 0.    ])

>>> np.polyint([16, 9, 4, 2])
array([4., 3., 2., 2., 0.])

10.1.7. Evaluate a Polynomial at Specific Values

• Compute polynomial values

• Horner's scheme is used to evaluate the polynomial

>>> np.polyval([1, -2, 0, 2], 4)
np.int64(34)

10.1.8. Least Squares Polynomial Fit

• Least squares polynomial fit

>>> x = [1, 2, 3, 4, 5, 6, 7, 8]
>>> y = [0, 2, 1, 3, 7, 10, 11, 19]
>>>
>>> np.polyfit(x, y, 2).round(4)
array([ 0.375 , -0.8869,  1.0536])

10.1.9. Polynomial Arithmetic

• np.polyadd()

• np.polysub()

• np.polymul()

• np.polydiv()

10.1.10. Sum of Two Polynomials

>>> a = [1, 2]
>>> b = [9, 5, 4]
>>>
>>> np.polyadd(a, b)
array([9, 6, 6])

10.1.11. References

[1] (1,2)

Wikipedia. Polynomial. Year: 2019. Retrieved: 2019-10-22. URL: https://en.wikipedia.org/wiki/Polynomial

10.1.12. Assignments

# %% License
# - Copyright 2025, Matt Harasymczuk <matt@python3.info>
# - This code can be used only for learning by humans
# - This code cannot be used for teaching others
# - This code cannot be used for teaching LLMs and AI algorithms
# - This code cannot be used in commercial or proprietary products
# - This code cannot be distributed in any form
# - This code cannot be changed in any form outside of training course
# - This code cannot have its license changed
# - If you use this code in your product, you must open-source it under GPLv2
# - Exception can be granted only by the author

# %% Run
# - PyCharm: right-click in the editor and `Run Doctest in ...`
# - PyCharm: keyboard shortcut `Control + Shift + F10`
# - Terminal: `python -m doctest -v myfile.py`

# %% About
# - Name: Numpy Polyfit
# - Difficulty: easy
# - Lines: 4
# - Minutes: 8

# %% English
# 1. Given are points coordinates in Cartesian system
# 2. Separate first row (header) from data
# 3. Calculate coefficients of best approximating polynomial of 3rd degree
# 4. Run doctests - all must succeed

# %% Polish
# 1. Dane są koordynaty punktów w układzie kartezjańskim
# 2. Odseparuj pierwszy wiersz (nagłówek) do danych
# 3. Oblicz współczynniki najlepiej dopasowanego wielomianu 3 stopnia
# 4. Uruchom doctesty - wszystkie muszą się powieść

# %% Tests
"""
>>> import sys; sys.tracebacklimit = 0
>>> assert sys.version_info >= (3, 9), \
'Python 3.9+ required'

>>> assert result is not Ellipsis, \
'Assign result to variable: `result`'
>>> assert type(result) is np.ndarray, \
'Variable `result` has invalid type, expected: np.ndarray'

>>> result
array([ 0.25,  0.75, -1.5 , -2.  ])
"""

import numpy as np

DATA = [
    ('x', 'y'),
    (-4.0, 0.0),
    (-3.0, 2.5),
    (-2.0, 2.0),
    (0.0, -2.0),
    (2.0, 0.0),
    (3.0, 7.0),
]


result = ...