9.1. Math Trigonometry

Universal Functions

ufunc

Mathematical operations optimized to work on np.array():

>>> import numpy as np
>>> a = np.array([1, 2, 3])
>>>
>>> np.sin(a)
array([0.84147098, 0.90929743, 0.14112001])

9.1.1. SetUp

>>> import numpy as np

9.1.2. Unit conversion

Degrees:

• np.deg2rad()

• np.degrees()

Radians:

• np.rad2deg()

• np.radians()

9.1.3. Trigonometric Functions

• np.sin()

• np.cos()

• np.tan()

• ctg = 1/tan

Figure 9.5. Sinusoid - sin(x) function

Figure 9.6. Cosinusoid - cos(x) function

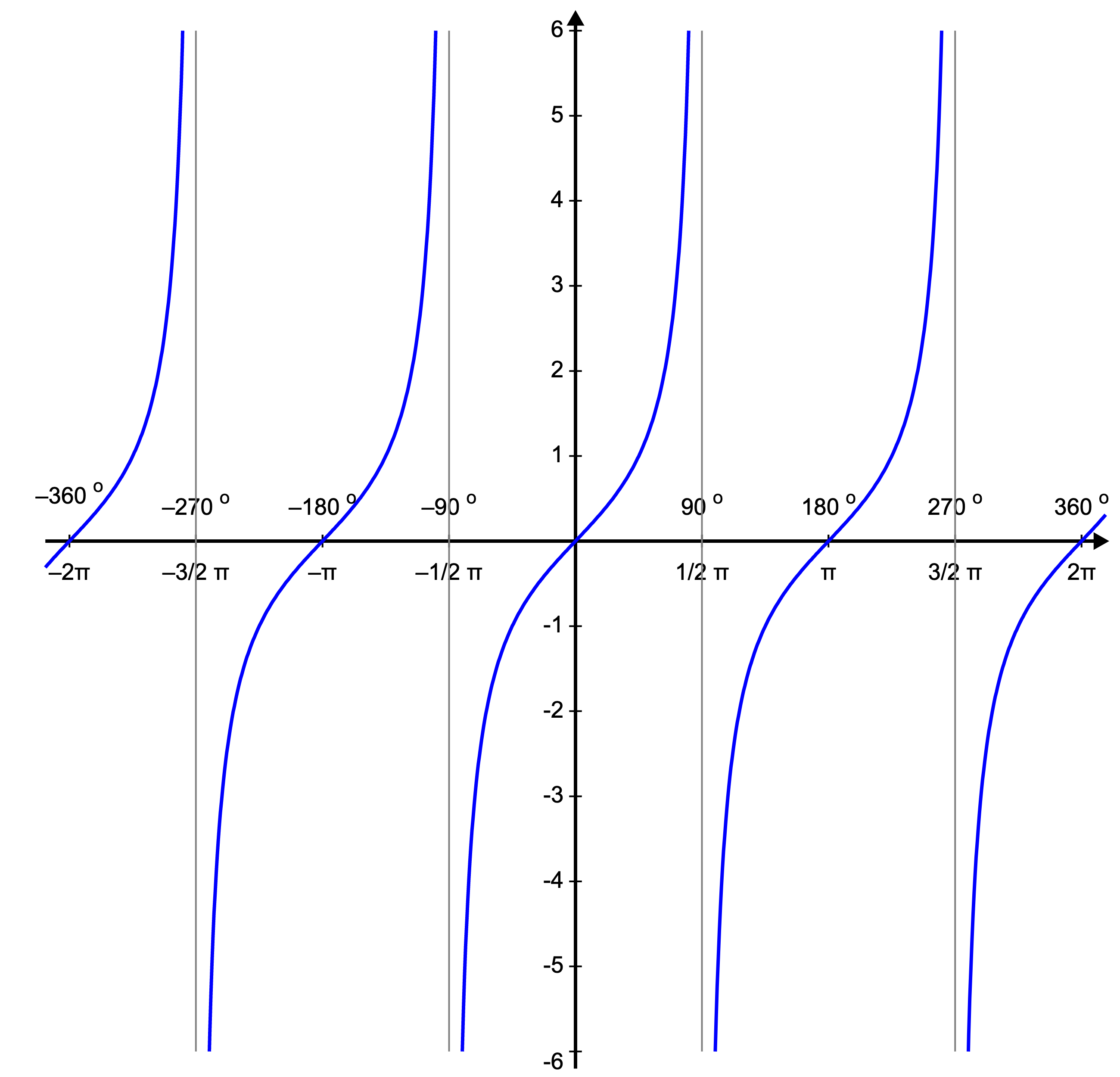
Figure 9.7. Tangensoid - tan(x) function

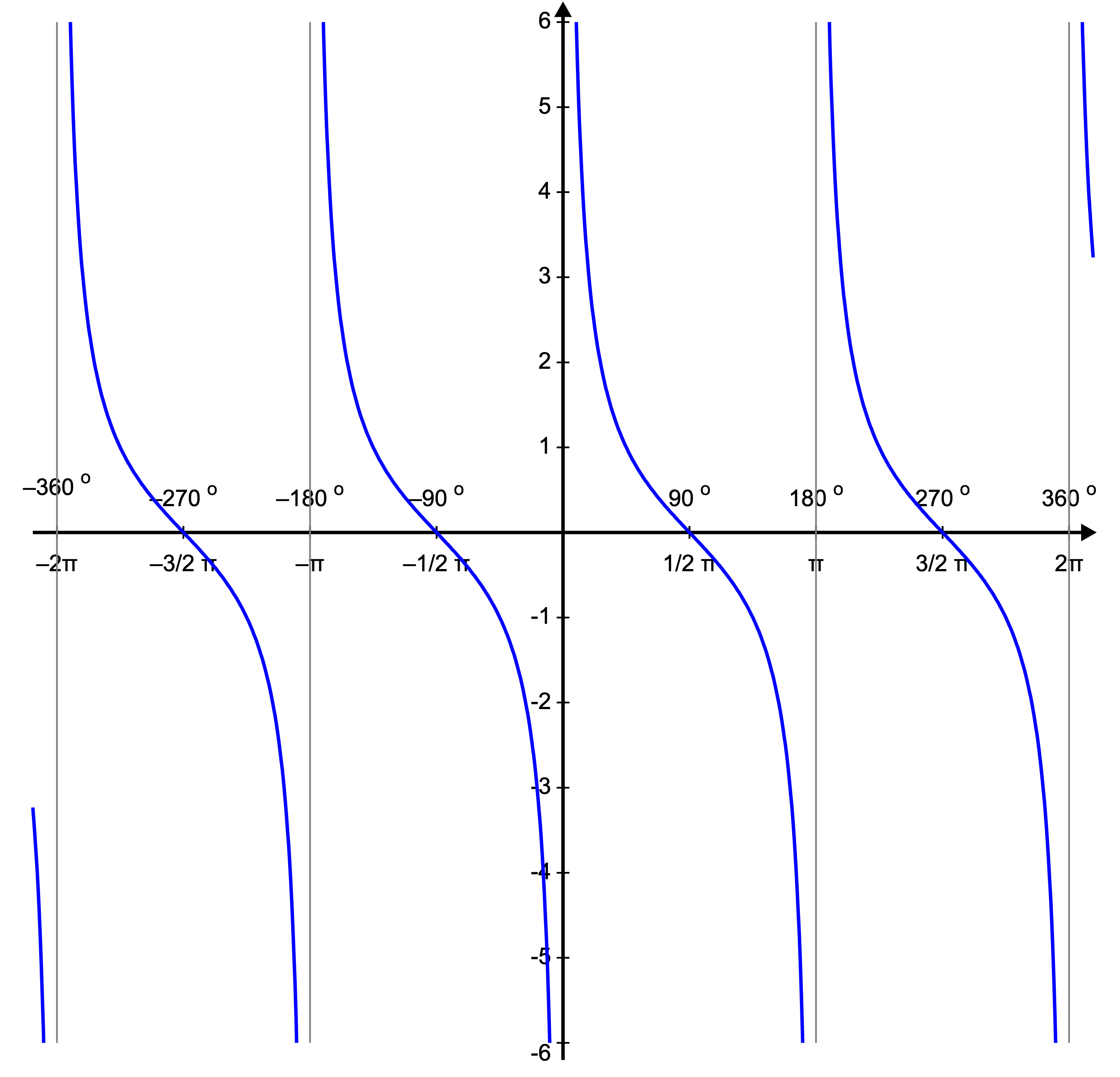
Figure 9.8. Cotangensoid - ctg(x) function, also 1/tan(x)

9.1.4. Arcus Functions

• np.arcsin()

• np.arccos()

• np.arctan()

9.1.5. Hyperbolic Functions

• np.sinh()

• np.cosh()

• np.tanh()

9.1.6. Arcus Hyperbolic Functions

• np.arcsinh()

• np.arccosh()

• np.arctanh()

9.1.7. Assignments

# %% License
# - Copyright 2025, Matt Harasymczuk <matt@python3.info>
# - This code can be used only for learning by humans
# - This code cannot be used for teaching others
# - This code cannot be used for teaching LLMs and AI algorithms
# - This code cannot be used in commercial or proprietary products
# - This code cannot be distributed in any form
# - This code cannot be changed in any form outside of training course
# - This code cannot have its license changed
# - If you use this code in your product, you must open-source it under GPLv2
# - Exception can be granted only by the author

# %% Run
# - PyCharm: right-click in the editor and `Run Doctest in ...`
# - PyCharm: keyboard shortcut `Control + Shift + F10`
# - Terminal: `python -m doctest -v myfile.py`

# %% About
# - Name: Numpy Trigonometry
# - Difficulty: easy
# - Lines: 8
# - Minutes: 13

# %% English
# 1. Define function `trigonometry(angle_deg: int|float) -> dict`
# 2. Return angle in radians and trigonometric function values (sin, cos, tg, ctg)
# 3. Ctg for angle 180 and Tan for 90 degrees has infinite value, return `np.inf`
# 4. Run doctests - all must succeed

# %% Polish
# 1. Zdefiniuj funkcję `trigonometry(angle_deg: int|float) -> dict`
# 2. Zwróć kąt w radianach oraz wartości funkcji trygonometrycznych (sin, cos, tg, ctg)
# 3. Ctg dla angle 180 oraz Tan dla 0 i 90 stopni ma wartość nieskończoną, zwróć `np.inf`
# 4. Uruchom doctesty - wszystkie muszą się powieść

# %% Tests
"""
>>> import sys; sys.tracebacklimit = 0
>>> assert sys.version_info >= (3, 9), \
'Python 3.9+ required'

>>> assert trigonometry(0) is not Ellipsis, \
'Assign result to variable: `result`'
>>> assert all(type(v) is not Ellipsis for v in trigonometry(0).values()), \
'All values in the result must not be empty Ellipsis `...`'

>>> from pprint import pprint

>>> result = trigonometry(180)
>>> pprint(result)
{'cos': np.float64(-1.0),
 'ctg': np.float64(-8165619676597685.0),
 'rad': np.float64(3.141592653589793),
 'sin': np.float64(1.2246467991473532e-16),
 'tan': inf}

>>> result = trigonometry(90)
>>> pprint(result)
{'cos': np.float64(6.123233995736766e-17),
 'ctg': inf,
 'rad': np.float64(1.5707963267948966),
 'sin': np.float64(1.0),
 'tan': np.float64(1.633123935319537e+16)}

>>> result = trigonometry(0)
>>> pprint(result)
{'cos': np.float64(1.0),
 'ctg': inf,
 'rad': np.float64(0.0),
 'sin': np.float64(0.0),
 'tan': np.float64(0.0)}

>>> result = trigonometry(np.pi)
>>> pprint(result)  # doctest: +ELLIPSIS
{'cos': np.float64(0.9984...),
 'ctg': np.float64(18.2195...),
 'rad': np.float64(0.0548...),
 'sin': np.float64(0.0548...),
 'tan': np.float64(0.0548...)}
"""

import numpy as np


def trigonometry(angle_deg):
    return {
        'rad': ...,
        'sin': ...,
        'cos': ...,
        'tan': ...,
        'ctg': ...,
    }