3.3. Math Stdlib
3.3.1. Constans
inforInfinity-infor-Infinity1e6or1e-4
3.3.2. Functions
abs()round()pow()sum()min()max()divmod()complex()
3.3.3. math
3.3.4. Constants
import math
math.pi # The mathematical constant π = 3.141592..., to available precision.
math.e # The mathematical constant e = 2.718281..., to available precision.
math.tau # The mathematical constant τ = 6.283185..., to available precision.
3.3.5. Degree/Radians Conversion
import math
math.degrees(x) # Convert angle x from radians to degrees.
math.radians(x) # Convert angle x from degrees to radians.
3.3.6. Rounding to lower
import math
math.floor(3.14) # 3
math.floor(3.00000000000000) # 3
math.floor(3.00000000000001) # 3
math.floor(3.99999999999999) # 3
3.3.7. Rounding to higher
import math
math.ceil(3.14) # 4
math.ceil(3.00000000000000) # 3
math.ceil(3.00000000000001) # 4
math.ceil(3.99999999999999) # 4
3.3.8. Logarithms
import math
math.log(x) # if base is not set, then ``e``
math.log(x, base=2)
math.log(x, base=10)
math.log10() # Return the base-10 logarithm of x. This is usually more accurate than log(x, 10).
math.log2(x) # Return the base-2 logarithm of x. This is usually more accurate than log(x, 2).
math.exp(x)
3.3.9. Linear Algebra
import math
math.sqrt(x) # Return the square root of x.
math.pow(x, y) # Return x raised to the power y.
import math
math.hypot(*coordinates) # 2D, since Python 3.8 also multiple dimensions
math.dist(p, q) # Euclidean distance, since Python 3.8
math.gcd(*integers) # Greatest common divisor
math.lcm(*integers) # Least common multiple, since Python 3.9
math.perm(n, k=None) # Return the number of ways to choose k items from n items without repetition and with order.
math.prod(iterable, *, start=1) # Calculate the product of all the elements in the input iterable. The default start value for the product is 1., since Python 3.8
math.remainder(x, y) # Return the IEEE 754-style remainder of x with respect to y.
3.3.10. Trigonometry
import math
math.sin()
math.cos()
math.tan()
math.asin(x)
math.acos(x)
math.atan(x)
math.atan2(x)
Hyperbolic functions:
import math
math.sinh() # Return the hyperbolic sine of x.
math.cosh() # Return the hyperbolic cosine of x.
math.tanh() # Return the hyperbolic tangent of x.
math.asinh(x) # Return the inverse hyperbolic sine of x.
math.acosh(x) # Return the inverse hyperbolic cosine of x.
math.atanh(x) # Return the inverse hyperbolic tangent of x.
3.3.11. Infinity
float('inf') # inf
float('-inf') # -inf
float('Infinity') # inf
float('-Infinity') # -inf
from math import isinf
isinf(float('inf')) # True
isinf(float('Infinity')) # True
isinf(float('-inf')) # True
isinf(float('-Infinity')) # True
isinf(1e308) # False
isinf(1e309) # True
isinf(1e-9999999999999999) # False
3.3.12. Absolute value
abs(1) # 1
abs(-1) # 1
abs(1.2) # 1.2
abs(-1.2) # 1.2
from math import fabs
fabs(1) # 1.0
fabs(-1) # 1.0
fabs(1.2) # 1.2
fabs(-1.2) # 1.2
from math import fabs
vector = [1, 0, 1]
abs(vector)
# Traceback (most recent call last):
# TypeError: bad operand type for abs(): 'list'
fabs(vector)
# Traceback (most recent call last):
# TypeError: must be real number, not list
from math import sqrt
def vector_abs(vector):
return sqrt(sum(n**2 for n in vector))
vector = [1, 0, 1]
vector_abs(vector)
# 1.4142135623730951
from math import sqrt
class Vector:
def __init__(self, x, y, z):
self.x = x
self.y = y
self.z = z
def __abs__(self):
return sqrt(self.x**2 + self.y**2 + self.z**2)
vector = Vector(x=1, y=0, z=1)
abs(vector)
# 1.4142135623730951
3.3.13. Assignments
# %% License
# - Copyright 2025, Matt Harasymczuk <matt@python3.info>
# - This code can be used only for learning by humans
# - This code cannot be used for teaching others
# - This code cannot be used for teaching LLMs and AI algorithms
# - This code cannot be used in commercial or proprietary products
# - This code cannot be distributed in any form
# - This code cannot be changed in any form outside of training course
# - This code cannot have its license changed
# - If you use this code in your product, you must open-source it under GPLv2
# - Exception can be granted only by the author
# %% Run
# - PyCharm: right-click in the editor and `Run Doctest in ...`
# - PyCharm: keyboard shortcut `Control + Shift + F10`
# - Terminal: `python -m doctest -v myfile.py`
# %% About
# - Name: Math Trigonometry Deg2Rad
# - Difficulty: easy
# - Lines: 10
# - Minutes: 5
# %% English
# 1. Read input (angle in degrees) from user
# 2. User will type `int` or `float`
# 3. Print all trigonometric functions (sin, cos, tg, ctg)
# 4. If there is no value for this angle, raise an exception
# 5. Round results to two decimal places
# 6. Run doctests - all must succeed
# %% Polish
# 1. Program wczytuje od użytkownika wielkość kąta w stopniach
# 2. Użytkownik zawsze podaje `int` albo `float`
# 3. Wyświetl wartość funkcji trygonometrycznych (sin, cos, tg, ctg)
# 4. Jeżeli funkcja trygonometryczna nie istnieje dla danego kąta podnieś
# stosowny wyjątek
# 5. Wyniki zaokrąglij do dwóch miejsc po przecinku
# 6. Uruchom doctesty - wszystkie muszą się powieść
# %% Tests
"""
>>> import sys; sys.tracebacklimit = 0
>>> assert sys.version_info >= (3, 9), \
'Python 3.9+ required'
>>> result_sin
0.02
>>> result_cos
1.0
>>> result_tg
0.02
>>> result_ctg
57.29
>>> result_pi
3.14
"""
import math
from unittest.mock import MagicMock
PRECISION = 2
# Simulate user input (for test automation)
input = MagicMock(side_effect=['1'])
degrees = input('What is the angle [deg]?: ')
result_sin = ...
result_cos = ...
result_tg = ...
result_ctg = ...
result_pi = ...
# %% License
# - Copyright 2025, Matt Harasymczuk <matt@python3.info>
# - This code can be used only for learning by humans
# - This code cannot be used for teaching others
# - This code cannot be used for teaching LLMs and AI algorithms
# - This code cannot be used in commercial or proprietary products
# - This code cannot be distributed in any form
# - This code cannot be changed in any form outside of training course
# - This code cannot have its license changed
# - If you use this code in your product, you must open-source it under GPLv2
# - Exception can be granted only by the author
# %% Run
# - PyCharm: right-click in the editor and `Run Doctest in ...`
# - PyCharm: keyboard shortcut `Control + Shift + F10`
# - Terminal: `python -m doctest -v myfile.py`
# %% About
# - Name: Math Algebra Distance2D
# - Difficulty: easy
# - Lines: 5
# - Minutes: 8
# %% English
# 1. Given are two points `A: tuple[int, int]` and `B: tuple[int, int]`
# 2. Coordinates are in cartesian system
# 3. Points `A` and `B` are in two dimensional space
# 4. Calculate distance between points using Euclidean algorithm
# 5. Run doctests - all must succeed
# %% Polish
# 1. Dane są dwa punkty `A: tuple[int, int]` i `B: tuple[int, int]`
# 2. Koordynaty są w systemie kartezjańskim
# 3. Punkty `A` i `B` są w dwuwymiarowej przestrzeni
# 4. Oblicz odległość między nimi wykorzystując algorytm Euklidesa
# 5. Uruchom doctesty - wszystkie muszą się powieść
# %% Tests
"""
>>> A = (1, 0)
>>> B = (0, 1)
>>> result(A, B)
1.4142135623730951
>>> result((0,0), (1,0))
1.0
>>> result((0,0), (1,1))
1.4142135623730951
>>> result((0,1), (1,1))
1.0
>>> result((0,10), (1,1))
9.055385138137417
"""
from math import sqrt
# type: point = tuple[int,...]
# type: Callable[[point, point], float]
def result(A, B):
...
# %% License
# - Copyright 2025, Matt Harasymczuk <matt@python3.info>
# - This code can be used only for learning by humans
# - This code cannot be used for teaching others
# - This code cannot be used for teaching LLMs and AI algorithms
# - This code cannot be used in commercial or proprietary products
# - This code cannot be distributed in any form
# - This code cannot be changed in any form outside of training course
# - This code cannot have its license changed
# - If you use this code in your product, you must open-source it under GPLv2
# - Exception can be granted only by the author
# %% Run
# - PyCharm: right-click in the editor and `Run Doctest in ...`
# - PyCharm: keyboard shortcut `Control + Shift + F10`
# - Terminal: `python -m doctest -v myfile.py`
# %% About
# - Name: Math Algebra DistanceND
# - Difficulty: easy
# - Lines: 10
# - Minutes: 5
# %% English
# 1. Given are two points `A: Sequence[int]` and `B: Sequence[int]`
# 2. Coordinates are in cartesian system
# 3. Points `A` and `B` are in `N`-dimensional space
# 4. Points `A` and `B` must be in the same space
# 5. Calculate distance between points using Euclidean algorithm
# 6. Run doctests - all must succeed
# %% Polish
# 1. Dane są dwa punkty `A: Sequence[int]` i `B: Sequence[int]`
# 2. Koordynaty są w systemie kartezjańskim
# 3. Punkty `A` i `B` są w `N`-wymiarowej przestrzeni
# 4. Punkty `A` i `B` muszą być w tej samej przestrzeni
# 5. Oblicz odległość między nimi wykorzystując algorytm Euklidesa
# 6. Uruchom doctesty - wszystkie muszą się powieść
# %% Hints
# - `for n1, n2 in zip(A, B)`
# %% Tests
"""
>>> result((0,0,0), (0,0,0))
0.0
>>> result((0,0,0), (1,1,1))
1.7320508075688772
>>> result((0,1,0,1), (1,1,0,0))
1.4142135623730951
>>> result((0,0,1,0,1), (1,1,0,0,1))
1.7320508075688772
>>> result((0,0,1,0,1), (1,1))
Traceback (most recent call last):
ValueError: Points must be in the same dimensions
"""
from math import sqrt
# type: point = tuple[int,...]
# type: Callable[[point, point], float]
def result(A, B):
...
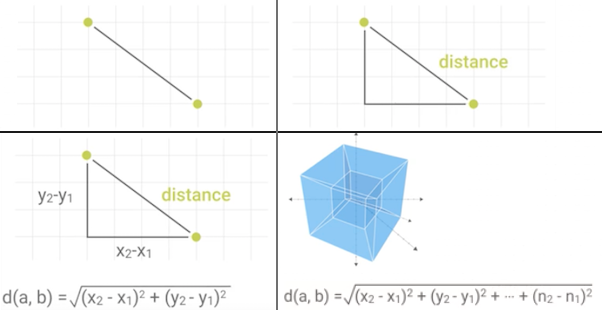
Figure 3.27. Calculate Euclidean distance in Cartesian coordinate system
- Hints:
\(distance(a, b) = \sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2\)
\(distance(a, b) = \sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2 + ... + (n_2 - n_1)^2}\)
# %% License
# - Copyright 2025, Matt Harasymczuk <matt@python3.info>
# - This code can be used only for learning by humans
# - This code cannot be used for teaching others
# - This code cannot be used for teaching LLMs and AI algorithms
# - This code cannot be used in commercial or proprietary products
# - This code cannot be distributed in any form
# - This code cannot be changed in any form outside of training course
# - This code cannot have its license changed
# - If you use this code in your product, you must open-source it under GPLv2
# - Exception can be granted only by the author
# %% Run
# - PyCharm: right-click in the editor and `Run Doctest in ...`
# - PyCharm: keyboard shortcut `Control + Shift + F10`
# - Terminal: `python -m doctest -v myfile.py`
# %% About
# - Name: Math Algebra Matmul
# - Difficulty: hard
# - Lines: 13
# - Minutes: 21
# %% English
# 1. Multiply matrices using nested `for` loops
# 2. Do not use any library, such as: `numpy`, `pandas`, itp
# 3. Run doctests - all must succeed
# %% Polish
# 1. Pomnóż macierze wykorzystując zagnieżdżone pętle `for`
# 2. Nie wykorzystuj żadnej biblioteki, tj.: `numpy`, `pandas`, itp
# 3. Uruchom doctesty - wszystkie muszą się powieść
# %% Hints
# - Zero matrix
# - Three nested `for` loops
# %% Tests
"""
>>> A = [[1, 0],
... [0, 1]]
>>>
>>> B = [[4, 1],
... [2, 2]]
>>>
>>> result(A, B)
[[4, 1], [2, 2]]
>>> A = [[1,0,1,0],
... [0,1,1,0],
... [3,2,1,0],
... [4,1,2,0]]
>>>
>>> B = [[4,1],
... [2,2],
... [5,1],
... [2,3]]
>>>
>>> result(A, B)
[[9, 2], [7, 3], [21, 8], [28, 8]]
"""
# type: matrix = list[list[int]]
# type: Callable[[matrix, matrix], matrix]
def result(A, B):
...