6.3. Operations Broadcasting

Vector

Broadcasting

Matrix Multiplication

6.3.1. SetUp

>>> import numpy as np

6.3.2. Broadcasting Rules

• Source [1]

1. Operations between multiple array objects are first checked for proper shape match

2. Mathematical operators (+, -, *, /, exp, log, ...) apply element by element, on values

3. Reduction operations (mean, std, skew, kurt, sum, prod, ...) apply to whole array, unless an axis is specified

4. Missing values propagate, unless explicitly ignored (nanmean, nansum, ...)

6.3.3. Addition

>>> a = np.array([[1, 2, 3], [4, 5, 6]])
>>> b = np.array([[4, 5, 6], [7, 8, 9]])
>>> c = np.array([1, 2, 3])
>>> d = np.array([4, 5])
>>>
>>> a + a
array([[ 2,  4,  6],
       [ 8, 10, 12]])
>>>
>>> a + b
array([[ 5,  7,  9],
       [11, 13, 15]])
>>>
>>> a + c
array([[2, 4, 6],
       [5, 7, 9]])
>>>
>>> a + d
Traceback (most recent call last):
ValueError: operands could not be broadcast together with shapes (2,3) (2,)

6.3.4. Subtraction

>>> a = np.array([[1, 2, 3], [4, 5, 6]])
>>> b = np.array([[4, 5, 6], [7, 8, 9]])
>>> c = np.array([1, 2, 3])
>>> d = np.array([4, 5])
>>>
>>> a - a
array([[0, 0, 0],
       [0, 0, 0]])
>>>
>>> a - b
array([[-3, -3, -3],
       [-3, -3, -3]])
>>>
>>> a - c
array([[0, 0, 0],
       [3, 3, 3]])
>>>
>>> a - d
Traceback (most recent call last):
ValueError: operands could not be broadcast together with shapes (2,3) (2,)

6.3.5. True Division

>>> a = np.array([[1, 2, 3], [4, 5, 6]])
>>> b = np.array([[4, 5, 6], [7, 8, 9]])
>>> c = np.array([1, 2, 3])
>>> d = np.array([4, 5])
>>>
>>> a / a
array([[1., 1., 1.],
       [1., 1., 1.]])
>>>
>>> a / b
array([[0.25      , 0.4       , 0.5       ],
       [0.57142857, 0.625     , 0.66666667]])
>>>
>>> a / c
array([[1. , 1. , 1. ],
       [4. , 2.5, 2. ]])
>>>
>>> a / d
Traceback (most recent call last):
ValueError: operands could not be broadcast together with shapes (2,3) (2,)

6.3.6. Floor Division

>>> a = np.array([[1, 2, 3], [4, 5, 6]])
>>> b = np.array([[4, 5, 6], [7, 8, 9]])
>>> c = np.array([1, 2, 3])
>>> d = np.array([4, 5])
>>>
>>> a // a
array([[1, 1, 1],
       [1, 1, 1]])
>>>
>>> a // b
array([[0, 0, 0],
       [0, 0, 0]])
>>>
>>> a // c
array([[1, 1, 1],
       [4, 2, 2]])
>>>
>>> a // d
Traceback (most recent call last):
ValueError: operands could not be broadcast together with shapes (2,3) (2,)

6.3.7. Modulo

>>> a = np.array([[1, 2, 3], [4, 5, 6]])
>>> b = np.array([[4, 5, 6], [7, 8, 9]])
>>> c = np.array([1, 2, 3])
>>> d = np.array([4, 5])
>>>
>>> a % a
array([[0, 0, 0],
       [0, 0, 0]])
>>>
>>> a % b
array([[1, 2, 3],
       [4, 5, 6]])
>>>
>>> a % c
array([[0, 0, 0],
       [0, 1, 0]])
>>>
>>> a % d
Traceback (most recent call last):
ValueError: operands could not be broadcast together with shapes (2,3) (2,)

6.3.8. Power

>>> a = np.array([[1, 2, 3], [4, 5, 6]])
>>> b = np.array([[4, 5, 6], [7, 8, 9]])
>>> c = np.array([1, 2, 3])
>>> d = np.array([4, 5])
>>>
>>> a ** a
array([[    1,     4,    27],
       [  256,  3125, 46656]])
>>>
>>> a ** b
array([[       1,       32,      729],
       [   16384,   390625, 10077696]])
>>>
>>> a ** c
array([[  1,   4,  27],
       [  4,  25, 216]])
>>>
>>> a ** d
Traceback (most recent call last):
ValueError: operands could not be broadcast together with shapes (2,3) (2,)

6.3.9. Root

>>> a = np.array([[1, 2, 3], [4, 5, 6]])
>>> b = np.array([[4, 5, 6], [7, 8, 9]])
>>> c = np.array([1, 2, 3])
>>> d = np.array([4, 5])
>>>
>>> a ** (1/a)
array([[1.        , 1.41421356, 1.44224957],
       [1.41421356, 1.37972966, 1.34800615]])
>>>
>>> a ** (1/b)
array([[1.        , 1.14869835, 1.20093696],
       [1.21901365, 1.22284454, 1.22028494]])
>>>
>>> a ** (1/c)
array([[1.        , 1.41421356, 1.44224957],
       [4.        , 2.23606798, 1.81712059]])
>>>
>>> a ** (1/d)
Traceback (most recent call last):
ValueError: operands could not be broadcast together with shapes (2,3) (2,)

6.3.10. Array Multiplication

• Multiplication * remains elementwise

• Does not correspond to matrix multiplication

>>> a = np.array([[1, 2, 3], [4, 5, 6]])
>>> b = np.array([[4, 5, 6], [7, 8, 9]])
>>> c = np.array([1, 2, 3])
>>> d = np.array([4, 5])
>>>
>>> a * a
array([[ 1,  4,  9],
       [16, 25, 36]])
>>>
>>> a * b
array([[ 4, 10, 18],
       [28, 40, 54]])
>>>
>>> a * c
array([[ 1,  4,  9],
       [ 4, 10, 18]])
>>>
>>> a * d
Traceback (most recent call last):
ValueError: operands could not be broadcast together with shapes (2,3) (2,)

6.3.11. Matrix Multiplication

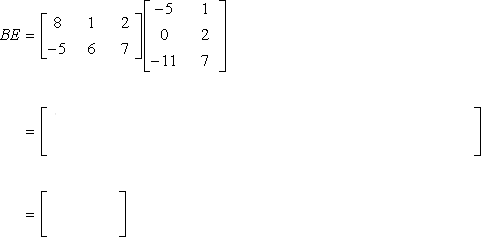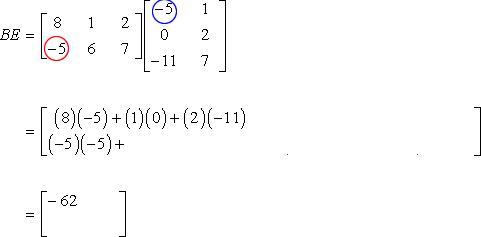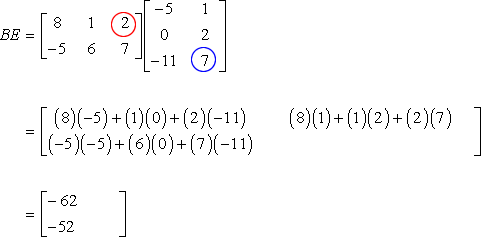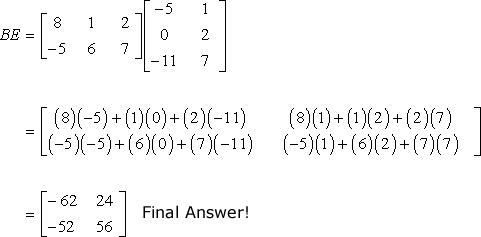
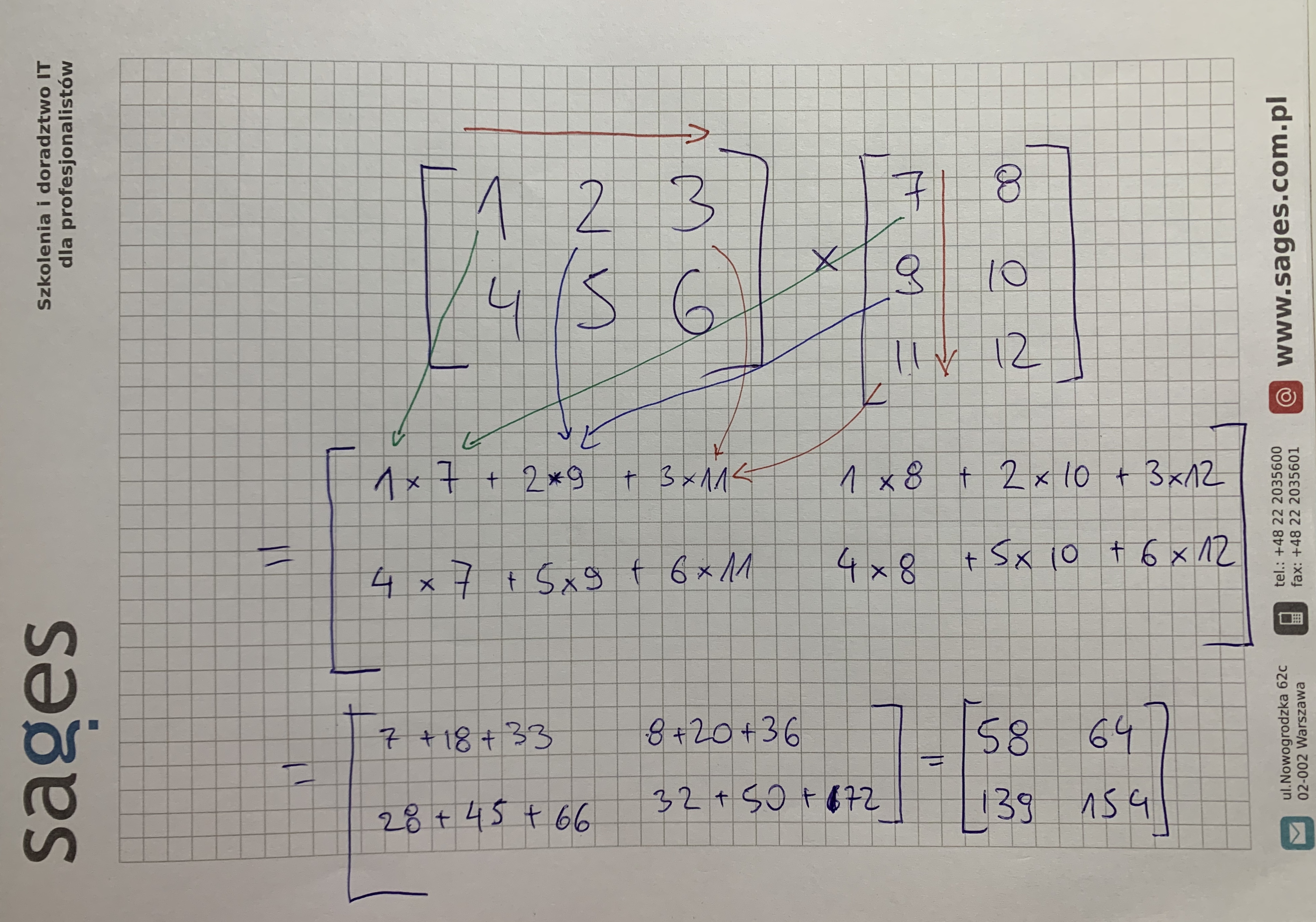
>>> a = np.array([[1, 2, 3],
...               [4, 5, 6]])
>>>
>>> b = np.array([[1, 2],
...               [3, 4],
...               [5, 6]])
>>>
>>> a @ b
array([[22, 28],
       [49, 64]])

>>> a = np.array([[1, 2, 3],
...               [4, 5, 6]])
>>>
>>> b = np.array([[4, 5, 6],
...               [7, 8, 9]])
>>>
>>> a @ b
Traceback (most recent call last):
ValueError: matmul: Input operand 1 has a mismatch in its core dimension 0, with gufunc signature (n?,k),(k,m?)->(n?,m?) (size 2 is different from 3)

6.3.12. Dot

• np.dot()

• If either a or b is 0-D (scalar), it is equivalent to multiply and using numpy.multiply(a, b) or a * b is preferred.

• If both a and b are 1-D arrays, it is inner product of vectors (without complex conjugation).

• If both a and b are 2-D arrays, it is matrix multiplication, but using matmul or a @ b is preferred.

• If a is an N-D array and b is a 1-D array, it is a sum product over the last axis of a and b.

• If a is an N-D array and b is an M-D array (where M>=2), it is a sum product over the last axis of a and the second-to-last axis of b: dot(a, b)[i,j,k,m] = sum(a[i,j,:] * b[k,:,m])

>>> a = np.array([1, 2, 3], float)
>>> b = np.array([0, 1, 1], float)
>>>
>>> np.dot(a, b)
np.float64(5.0)

>>> a = np.array([[0, 1], [2, 3]], float)
>>> b = np.array([2, 3], float)
>>> c = np.array([[1, 1], [4, 0]], float)
>>>
>>> np.dot(b, a)
array([ 6., 11.])
>>>
>>> np.dot(a, b)
array([ 3., 13.])
>>>
>>> np.dot(a, c)
array([[ 4.,  0.],
       [14.,  2.]])
>>>
>>> np.dot(c, a)
array([[2., 4.],
       [0., 4.]])

6.3.13. References

[1]

Alex Chabot-Leclerc. Introduction to Numerical Computing with NumPy: Broadcasting Rules. Year: 2019. Retrieved: 2019-11-31. URL: https://youtu.be/ZB7BZMhfPgk?t=5142

6.3.14. Assignments

# %% About
# - Name: Numpy Broadcasting Arithmetic
# - Difficulty: easy
# - Lines: 4
# - Minutes: 3

# %% License
# - Copyright 2025, Matt Harasymczuk <matt@python3.info>
# - This code can be used only for learning by humans
# - This code cannot be used for teaching others
# - This code cannot be used for teaching LLMs and AI algorithms
# - This code cannot be used in commercial or proprietary products
# - This code cannot be distributed in any form
# - This code cannot be changed in any form outside of training course
# - This code cannot have its license changed
# - If you use this code in your product, you must open-source it under GPLv2
# - Exception can be granted only by the author

# %% English
# 1. Define `a: np.ndarray` with square root of each element in `A`
# 2. Define `b: np.ndarray` with square root of each element in `B`
# 3. Define `c: np.ndarray` with second power (square) of each element in `C`
# 4. Add elements from `a` to `b`
# 5. Multiply the result by `c`
# 6. Run doctests - all must succeed

# %% Polish
# 1. Zdefiniuj `a: np.ndarray` z pierwiastkiem kwadratowym każdego elementu `A`
# 2. Zdefiniuj `b: np.ndarray` z pierwiastkiem kwadratowym każdego elementu `B`
# 3. Zdefiniuj `c: np.ndarray` z drugą potęgą (kwadratem) każdego z elementu w `C`
# 4. Dodaj elementy z `a` do `b`
# 5. Przemnóż wynik przez `c`
# 6. Uruchom doctesty - wszystkie muszą się powieść

# %% Doctests
"""
>>> import sys; sys.tracebacklimit = 0
>>> assert sys.version_info >= (3, 9), \
'Python 3.9+ required'

>>> assert result is not Ellipsis, \
'Assign result to variable: `result`'
>>> assert type(result) is np.ndarray, \
'Variable `result` has invalid type, expected: np.ndarray'

>>> result
array([[ 1.41421356,  2.73205081],
       [45.254834  ,  0.        ]])
"""

# %% Run
# - PyCharm: right-click in the editor and `Run Doctest in ...`
# - PyCharm: keyboard shortcut `Control + Shift + F10`
# - Terminal: `python -m doctest -v myfile.py`

# %% Imports
import numpy as np

# %% Types
a: np.ndarray
b: np.ndarray
c: np.ndarray
result: np.ndarray

# %% Data
A = np.array([[0, 1], [2, 3]], dtype='float')
B = np.array([2, 3], dtype='float')
C = np.array([[1, 1], [4, 0]], dtype='float')

# %% Result
a = ...
b = ...
c = ...
result = ...

# %% About
# - Name: Numpy Broadcasting Type Cast
# - Difficulty: easy
# - Lines: 2
# - Minutes: 3

# %% License
# - Copyright 2025, Matt Harasymczuk <matt@python3.info>
# - This code can be used only for learning by humans
# - This code cannot be used for teaching others
# - This code cannot be used for teaching LLMs and AI algorithms
# - This code cannot be used in commercial or proprietary products
# - This code cannot be distributed in any form
# - This code cannot be changed in any form outside of training course
# - This code cannot have its license changed
# - If you use this code in your product, you must open-source it under GPLv2
# - Exception can be granted only by the author

# %% English
# 1. For given: `a: np.ndarray`, `b: np.ndarray` (see below)
# 2. Add `a` and `b`
# 3. Add `b` and `a`
# 4. What happened?
# 5. Run doctests - all must succeed

# %% Polish
# 1. Dla danych: `a: np.ndarray`, `b: np.ndarray` (patrz sekcja input)
# 2. Dodaj `a` i `b`
# 3. Dodaj `b` i `a`
# 4. Co się stało?
# 5. Uruchom doctesty - wszystkie muszą się powieść

# %% Doctests
"""
>>> import sys; sys.tracebacklimit = 0
>>> assert sys.version_info >= (3, 9), \
'Python 3.9+ required'

>>> assert type(result_ab) is np.ndarray, \
'Variable `result_ab` has invalid type, expected: np.ndarray'
>>> assert type(result_ba) is np.ndarray, \
'Variable `result_ba` has invalid type, expected: np.ndarray'

>>> result_ab
array([[5, 1],
       [2, 3]])

>>> result_ba
array([[5, 1],
       [2, 3]])
"""

# %% Run
# - PyCharm: right-click in the editor and `Run Doctest in ...`
# - PyCharm: keyboard shortcut `Control + Shift + F10`
# - Terminal: `python -m doctest -v myfile.py`

# %% Imports
import numpy as np

# %% Types
result_ab: np.ndarray
result_ba: np.ndarray

# %% Data
a = np.array([[1, 0], [0, 1]])
b = [[4, 1], [2, 2]]

# %% Result
result_ab = ...
result_ba = ...

# %% About
# - Name: Numpy Broadcasting Matmul
# - Difficulty: easy
# - Lines: 4
# - Minutes: 3

# %% License
# - Copyright 2025, Matt Harasymczuk <matt@python3.info>
# - This code can be used only for learning by humans
# - This code cannot be used for teaching others
# - This code cannot be used for teaching LLMs and AI algorithms
# - This code cannot be used in commercial or proprietary products
# - This code cannot be distributed in any form
# - This code cannot be changed in any form outside of training course
# - This code cannot have its license changed
# - If you use this code in your product, you must open-source it under GPLv2
# - Exception can be granted only by the author

# %% English
# 1. For given: `a: np.ndarray`, `b: np.ndarray` (see below)
# 2. Multiply `a` and `b` using scalar multiplication
# 3. Multiply `a` and `b` using matrix multiplication
# 4. Multiply `b` and `a` using scalar multiplication
# 5. Multiply `b` and `a` using matrix multiplication
# 6. Discuss results
# 7. Run doctests - all must succeed

# %% Polish
# 1. Dla danych: `a: np.ndarray`, `b: np.ndarray` (patrz sekcja input)
# 2. Przemnóż `a` i `b` używając mnożenia skalarnego
# 3. Przemnóż `a` i `b` używając mnożenia macierzowego
# 4. Przemnóż `b` i `a` używając mnożenia skalarnego
# 5. Przemnóż `b` i `a` używając mnożenia macierzowego
# 6. Omów wyniki
# 7. Uruchom doctesty - wszystkie muszą się powieść

# %% Doctests
"""
>>> import sys; sys.tracebacklimit = 0
>>> assert sys.version_info >= (3, 9), \
'Python 3.9+ required'

>>> mul_ab(a, b)  # doctest: +NORMALIZE_WHITESPACE
Traceback (most recent call last):
ValueError: operands could not be broadcast together with shapes (4,4) (4,2)

>>> matmul_ab(a, b)
array([[ 9,  2],
       [ 7,  3],
       [21,  8],
       [28,  8]])

>>> mul_ba(b, a)  # doctest: +NORMALIZE_WHITESPACE
Traceback (most recent call last):
ValueError: operands could not be broadcast together with shapes (4,2) (4,4)

>>> matmul_ba(b, a)
Traceback (most recent call last):
ValueError: matmul: Input operand 1 has a mismatch in its core dimension 0, with gufunc signature (n?,k),(k,m?)->(n?,m?) (size 4 is different from 2)
"""

# %% Run
# - PyCharm: right-click in the editor and `Run Doctest in ...`
# - PyCharm: keyboard shortcut `Control + Shift + F10`
# - Terminal: `python -m doctest -v myfile.py`

# %% Imports
import numpy as np

# %% Types
from typing import Callable
mul_ab: Callable[[np.ndarray, np.ndarray], np.ndarray|Exception]
matmul_ab: Callable[[np.ndarray, np.ndarray], np.ndarray|Exception]
mul_ba: Callable[[np.ndarray, np.ndarray], np.ndarray|Exception]
matmul_ba: Callable[[np.ndarray, np.ndarray], np.ndarray|Exception]

# %% Data
a = np.array([[1, 0, 1, 0],
              [0, 1, 1, 0],
              [3, 2, 1, 0],
              [4, 1, 2, 0]])

b = np.array([
    [4, 1],
    [2, 2],
    [5, 1],
    [2, 3]])


# %% Result
def mul_ab(a, b):
    return ...

def matmul_ab(a, b):
    return ...

def mul_ba(b, a):
    return ...

def matmul_ba(b, a):
    return ...