9.6. Idiom Sorted

9.6.1. Problem

• Bubble sort

>>> data = [3, 1, 2]
>>>
>>> def mysorted(data):
...     result = data.copy()
...     n = len(data)
...     for i in range(n):
...         for j in range(n-i-1):
...             if result[j] > result[j+1]:
...                 result[j], result[j+1] = result[j+1], result[j]
...     return result
>>>
>>> mysorted(data)
[1, 2, 3]

9.6.2. Solution

>>> data = [3, 1, 2]
>>>
>>> sorted(data)
[1, 2, 3]

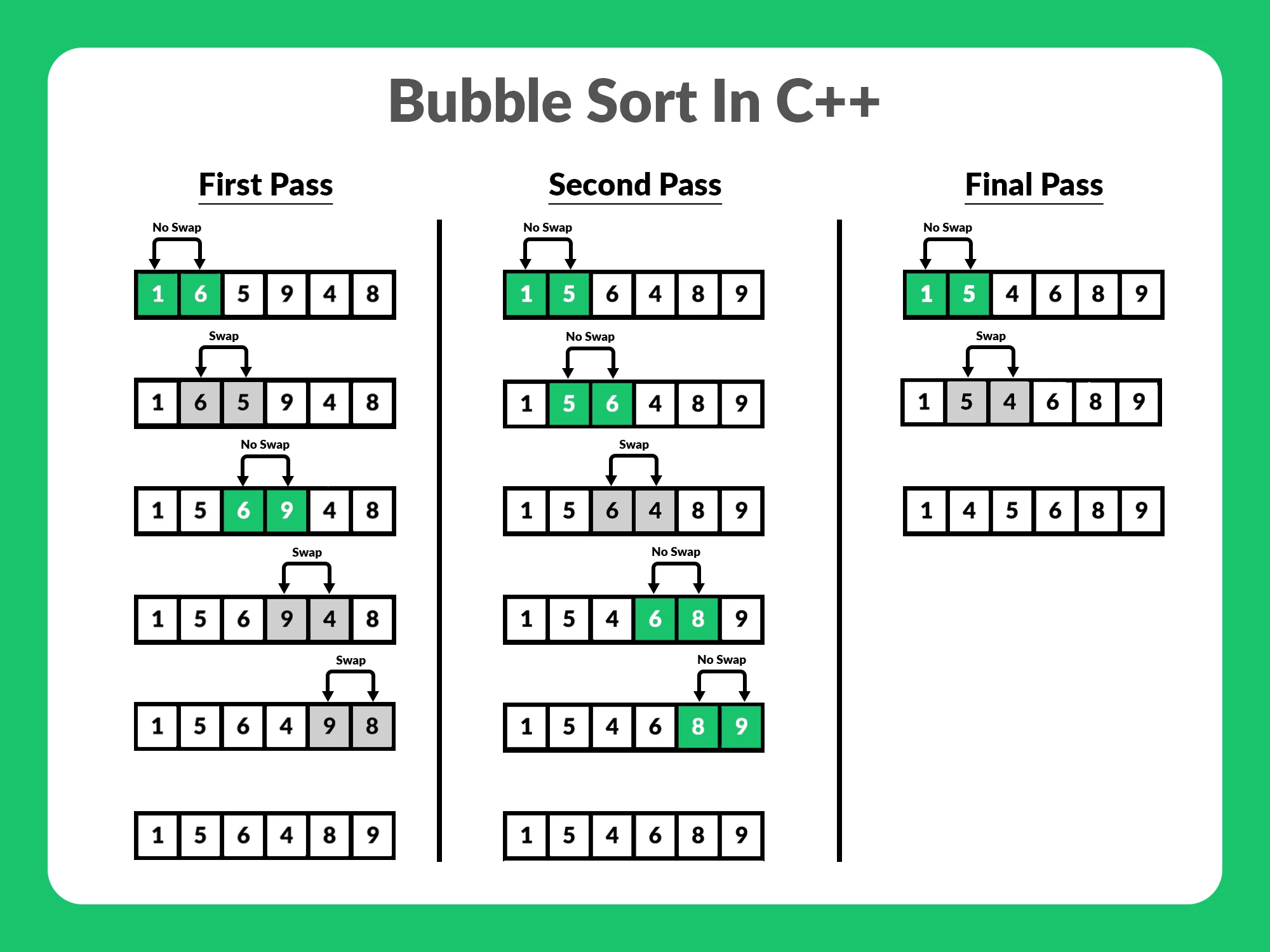
9.6.3. Bubble Sort

>>> def bubblesort(arr):
...     result = arr.copy()
...     n = len(arr)
...     for i in range(n):
...         for j in range(n-i-1):
...             if result[j] > result[j+1]:
...                 result[j], result[j+1] = result[j+1], result[j]
...     return result

9.6.4. Merge Sort

>>> def mergesort(arr):
...     if len(arr) <= 1:
...         return arr
...
...     mid = len(arr) // 2
...     left = mergesort(arr[:mid])
...     right = mergesort(arr[mid:])
...
...     result = []
...     i = j = 0
...
...     while i < len(left) and j < len(right):
...         if left[i] < right[j]:
...             result.append(left[i])
...             i += 1
...         else:
...             result.append(right[j])
...             j += 1
...
...     result.extend(left[i:])
...     result.extend(right[j:])
...     return result

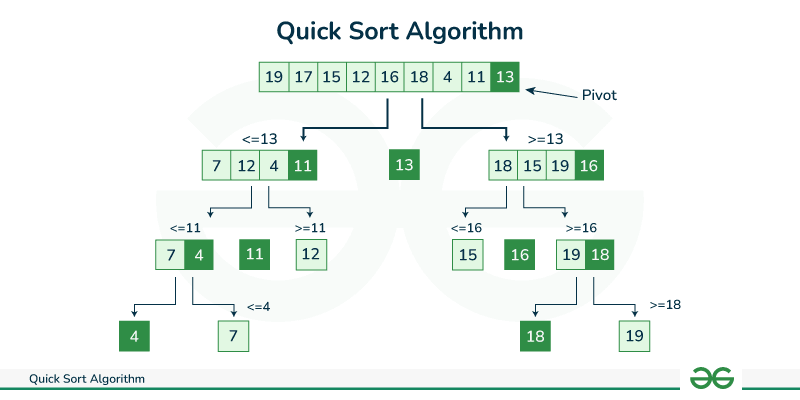
9.6.5. Quick Sort

>>> def quicksort(arr):
...     if len(arr) <= 1:
...         return arr
...
...     pivot = arr[len(arr) // 2]
...     left = [x for x in arr if x < pivot]
...     middle = [x for x in arr if x == pivot]
...     right = [x for x in arr if x > pivot]
...
...     return quicksort(left) + middle + quicksort(right)

9.6.6. Tim Sort

• Tim Peters

>>> def timsort(arr):
...     min_run = 32
...     n = len(arr)
...
...     def insertion_sort(arr, left, right):
...         for i in range(left + 1, right + 1):
...             key = arr[i]
...             j = i - 1
...             while j >= left and arr[j] > key:
...                 arr[j + 1] = arr[j]
...                 j -= 1
...             arr[j + 1] = key
...
...     def merge(arr, left, mid, right):
...         len1, len2 = mid - left + 1, right - mid
...         left_part, right_part = arr[left:left + len1], arr[mid + 1:mid + 1 + len2]
...
...         i = j = 0
...         k = left
...
...         while i < len1 and j < len2:
...             if left_part[i] <= right_part[j]:
...                 arr[k] = left_part[i]
...                 i += 1
...             else:
...                 arr[k] = right_part[j]
...                 j += 1
...             k += 1
...
...         while i < len1:
...             arr[k] = left_part[i]
...             i += 1
...             k += 1
...
...         while j < len2:
...             arr[k] = right_part[j]
...             j += 1
...             k += 1
...
...     for start in range(0, n, min_run):
...         end = min(start + min_run - 1, n - 1)
...         insertion_sort(arr, start, end)
...
...     size = min_run
...     while size < n:
...         for left in range(0, n, 2 * size):
...             mid = min(n - 1, left + size - 1)
...             right = min((left + 2 * size - 1), (n - 1))
...
...             if mid < right:
...                 merge(arr, left, mid, right)
...
...         size *= 2
...
...     return arr