16.1. Complexity¶
Computational Complexity
Memory Complexity
Cognitive Complexity
Cyclomatic Complexity
Big O notation [1]
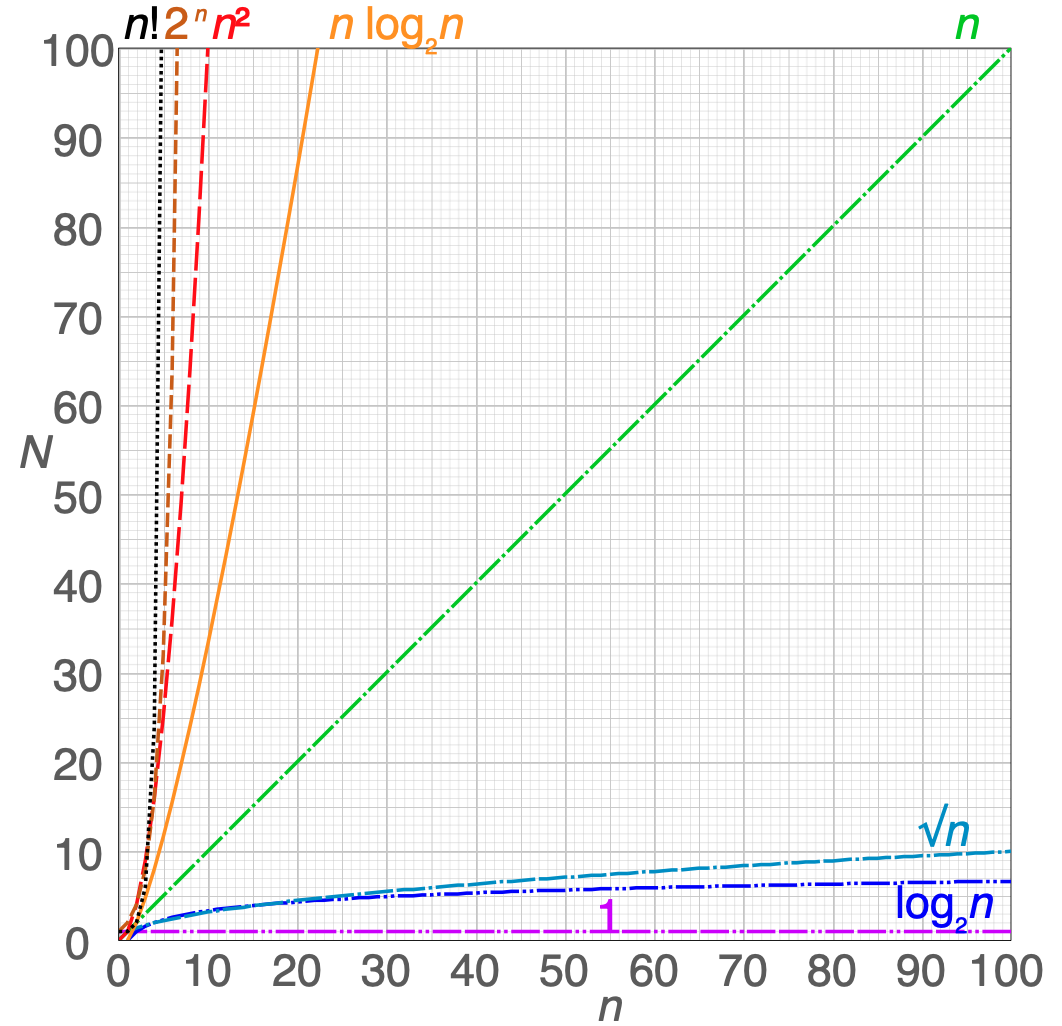
16.1.1. Computational Complexity¶
16.1.2. Memory Complexity¶
16.1.3. Cognitive Complexity¶
Measure of how difficult the application is to understand
Measure of how hard the control flow of a function is to understand
Functions with high Cognitive Complexity will be difficult to maintain.
16.1.4. Cyclomatic Complexity¶
Measures the minimum number of test cases required for full test coverage.
16.1.5. Big O notation¶
Most common:
O(sqrt_n)
O(log_n)
O(log2_n)
O(1)
O(n)
O(nlog2_n)
O(n^2)
O(2^n)
O(n!)
Running time (T(n)) |
Name |
Example algorithms |
|---|---|---|
|
constant time |
Finding the median value in a sorted array of numbersCalculating (−1)n |
|
inverse Ackermann time |
Amortized time per operation using a disjoint set |
|
iterated logarithmic time |
Distributed coloring of cycles |
|
log-logarithmic |
Amortized time per operation using a bounded priority queue |
|
logarithmic time |
Binary search |
|
polylogarithmic time |
|
|
fractional power |
Searching in a kd-tree |
|
linear time |
Finding the smallest or largest item in an unsorted array, Kadane's algorithm, linear search |
|
n log-star n time |
Seidel's polygon triangulation algorithm |
|
linearithmic time |
Fastest possible comparison sort; Fast Fourier transform |
|
quasilinear time |
|
|
quadratic time |
Bubble sort; Insertion sort; Direct convolution |
|
cubic time |
Naive multiplication of two n×n matrices. Calculating partial correlation |
|
polynomial time |
Karmarkar's algorithm for linear programming; AKS primality test |
|
quasi-polynomial time |
Best-known O(log2 n)-approximation algorithm for the directed Steiner tree problem |
|
sub-exponential time |
Best-known algorithm for integer factorization; formerly-best algorithm for graph isomorphism |
|
sub-exponential time |
Best-known algorithm for integer factorization; formerly-best algorithm for graph isomorphism |
|
exponential time (with linear exponent) |
Solving the traveling salesman problem using dynamic programming |
|
exponential time |
Solving matrix chain multiplication via brute-force search |
|
factorial time |
Solving the traveling salesman problem via brute-force search |
|
double exponential time |
Deciding the truth of a given statement in Presburger arithmetic |
16.1.6. References¶
16.1.7. Assignments¶
"""
* Assignment: Performance Compexity Segmentation
* Type: class assignment
* Complexity: easy
* Lines of code: 8 lines
* Time: 5 min
English:
1. Count occurrences of each group
2. Define groups:
a. `small` - numbers in range [0-3)
b. `medium` - numbers in range [3-7)
c. `large` - numbers in range [7-10)
3. Print `result: dict[str, int]`:
a. key - group
b. value - number of occurrences
4. Run doctests - all must succeed
Polish:
1. Policz wystąpienia każdej z group
2. Zdefiniuj grupy
a. `small` - liczby z przedziału <0-3)
b. `medium` - liczby z przedziału <3-7)
c. `large` - liczby z przedziału <7-10)
3. Wypisz `result: dict[str, int]`:
a. klucz - grupa
b. wartość - liczba wystąpień
4. Uruchom doctesty - wszystkie muszą się powieść
Tests:
>>> import sys; sys.tracebacklimit = 0
>>> type(result)
<class 'dict'>
>>> assert all(type(x) is str for x in result.keys())
>>> assert all(type(x) is int for x in result.values())
>>> result
{'small': 16, 'medium': 19, 'large': 15}
"""
DATA = [
1, 4, 6, 7, 4, 4, 4, 5, 1, 7, 0,
0, 6, 5, 0, 0, 9, 7, 0, 4, 4, 8,
2, 4, 0, 0, 1, 9, 1, 7, 8, 8, 9,
1, 3, 5, 6, 8, 2, 8, 1, 3, 9, 5,
4, 8, 1, 9, 6, 3,
]
# dict[str,int] number of digit occurrences in segments
result = {'small': 0, 'medium': 0, 'large': 0}
"""
* Assignment: Performance Compexity UniqueKeys
* Type: class assignment
* Complexity: easy
* Lines of code: 3 lines
* Time: 5 min
English:
1. Collect unique keys from all rows in one sequence `result`
2. Run doctests - all must succeed
Polish:
1. Zbierz unikalne klucze z wszystkich wierszy w jednej sekwencji `result`
2. Uruchom doctesty - wszystkie muszą się powieść
Hints:
* `row.keys()`
* Compare solutions with :ref:`Micro-benchmarking use case`
Tests:
>>> import sys; sys.tracebacklimit = 0
>>> result is not Ellipsis
True
>>> type(result) in (set, list, tuple, frozenset)
True
>>> sorted(result)
['petal_length', 'petal_width', 'sepal_length', 'sepal_width', 'species']
"""
DATA = [
{'sepal_length': 5.1, 'sepal_width': 3.5, 'species': 'setosa'},
{'petal_length': 4.1, 'petal_width': 1.3, 'species': 'versicolor'},
{'sepal_length': 6.3, 'petal_width': 1.8, 'species': 'virginica'},
{'sepal_length': 5.0, 'petal_width': 0.2, 'species': 'setosa'},
{'sepal_width': 2.8, 'petal_length': 4.1, 'species': 'versicolor'},
{'sepal_width': 2.9, 'petal_width': 1.8, 'species': 'virginica'},
]
# Unique keys from DATA dicts
# type: set[str]
result = ...
"""
* Assignment: Performance Compexity SplitTrainTest
* Type: homework
* Complexity: easy
* Lines of code: 4 lines
* Time: 5 min
English:
1. Using List Comprehension split `DATA` into:
a. `features_train: list[tuple]` - 60% of first features in `DATA`
b. `features_test: list[tuple]` - 40% of last features in `DATA`
c. `labels_train: list[str]` - 60% of first labels in `DATA`
d. `labels_test: list[str]` - 40% of last labels in `DATA`
2. In order to do so, calculate pivot point:
a. length of `DATA` times given percent (60% = 0.6)
b. remember, that slice indicies must be `int`, not `float`
c. for example: if dataset has 10 rows, then 6 rows will be for
training, and 4 rows for test
3. Run doctests - all must succeed
Polish:
1. Używając List Comprehension podziel `DATA` na:
a. `features_train: list[tuple]` - 60% pierwszych features w `DATA`
b. `features_test: list[tuple]` - 40% ostatnich features w `DATA`
c. `labels_train: list[str]` - 60% pierwszych labels w `DATA`
d. `labels_test: list[str]` - 40% ostatnich labels w `DATA`
2. Aby to zrobić, wylicz punkt podziału:
a. długość `DATA` razy zadany procent (60% = 0.6)
b. pamiętaj, że indeksy slice muszą być `int` a nie `float`
c. na przykład: if zbiór danych ma 10 wierszy, to 6 wierszy będzie
do treningu, a 4 do testów
3. Uruchom doctesty - wszystkie muszą się powieść
Tests:
>>> import sys; sys.tracebacklimit = 0
>>> assert type(features_train) is list, \
'make sure features_train is a list'
>>> assert type(features_test) is list, \
'make sure features_test is a list'
>>> assert type(labels_train) is list, \
'make sure labels_train is a list'
>>> assert type(labels_test) is list, \
'make sure labels_test is a list'
>>> assert all(type(x) is tuple for x in features_train), \
'all elements in features_train should be tuple'
>>> assert all(type(x) is tuple for x in features_test), \
'all elements in features_test should be tuple'
>>> assert all(type(x) is str for x in labels_train), \
'all elements in labels_train should be str'
>>> assert all(type(x) is str for x in labels_test), \
'all elements in labels_test should be str'
>>> features_train # doctest: +NORMALIZE_WHITESPACE
[(5.8, 2.7, 5.1, 1.9),
(5.1, 3.5, 1.4, 0.2),
(5.7, 2.8, 4.1, 1.3),
(6.3, 2.9, 5.6, 1.8),
(6.4, 3.2, 4.5, 1.5),
(4.7, 3.2, 1.3, 0.2)]
>>> features_test # doctest: +NORMALIZE_WHITESPACE
[(7.0, 3.2, 4.7, 1.4),
(7.6, 3.0, 6.6, 2.1),
(4.9, 3.0, 1.4, 0.2),
(4.9, 2.5, 4.5, 1.7)]
>>> labels_train
['virginica', 'setosa', 'versicolor', 'virginica', 'versicolor', 'setosa']
>>> labels_test
['versicolor', 'virginica', 'setosa', 'virginica']
"""
DATA = [
('sepal_length', 'sepal_width', 'petal_length', 'petal_width', 'species'),
(5.8, 2.7, 5.1, 1.9, 'virginica'),
(5.1, 3.5, 1.4, 0.2, 'setosa'),
(5.7, 2.8, 4.1, 1.3, 'versicolor'),
(6.3, 2.9, 5.6, 1.8, 'virginica'),
(6.4, 3.2, 4.5, 1.5, 'versicolor'),
(4.7, 3.2, 1.3, 0.2, 'setosa'),
(7.0, 3.2, 4.7, 1.4, 'versicolor'),
(7.6, 3.0, 6.6, 2.1, 'virginica'),
(4.9, 3.0, 1.4, 0.2, 'setosa'),
(4.9, 2.5, 4.5, 1.7, 'virginica'),
]
ratio = 0.6
header, *rows = DATA
split = int(len(rows) * ratio)
features_train = ...
features_test = ...
labels_train = ...
labels_test = ...